|
 DISPERSION
DISPERSION
The comparison of low frequency seismix data
with high frequency lab data (and sometimes medium frequency log
data) needs some discussion. The problem is called "dispersion",
which is the word used to describe the change in velocity versus
frequency of sound waves.
Biot's
original paper in 1956 pointed out that sonic velocity varied
with frequency and described a low frequency case (typically 5
to 35 KHz under normal reservoir conditions) and high frequency
case (typically 100 KHz to 1 MHx). Logging tools usually operate
in the low frequency range and conform to Biot's low frequency
case except in high porosity (> 35%).
Sonic
velocity measurements made under laboratory conditions are usually
made at 1 MHz because the core plugs are small and the high frequency
has a short enough wavelength to fully penetrate the sample. R.
A. Anderson's paper in 1984 gave graphs of both
high and low frequency data versus Wyllie porosity.
By comparing
the response of the two frequencies, we can create equations to
convert high frequency data to equivalent low frequency (logging
tool) values. Travel times taken at high frequency are too fast
(DTShi is too low).
1: DTScor = (DTShi - KS1) * 1.25 + KS1
2: DTCcor = (DTChi - KC1) * 1.02 + KC1
Where:
DTCcor = compressional sonic corrected for high frequency effect
(usec/ft or usec/m)
DTChi = lab measured compressional sonic reading (usec/ft or usec/m)
DTScor = shear sonic corrected for high frequency effect (usec/ft
or usec/m)
DTShi = lab measured shear sonic reading (usec/ft or usec/m)
Frequency and fluid effects on Sonic travel time (Anderson,
1984)
| |
Sandstone |
Limestone |
Dolomite |
| |
English |
Metric |
English |
Metric |
English |
Metric |
| KS1 |
88.8 |
291 |
90.2 |
296 |
79.2 |
260 |
| KC1 |
55.5 |
182 |
47.5 |
155 |
44.0 |
144 |
| |
|
|
|
|
|
|
|
Use
ONLY to convert lab measured high frequency (1 MHz) sonic data
to equivalent low frequency sonic log or seismic frequency data.
 GAS EFFECT ON ACOUSTIC DATA
GAS EFFECT ON ACOUSTIC DATA
At
shallow depths (low pressure gas), the Wyllie time average equation
described above is known to over-estimate the gas effect, so
alternate methods should be used. The
following material is taken from "Fluid and Frequency Effects on
Sonic Velocity", R. A. Anderson, SPWLA 1984. This paper
shows a rigorous calculation of compressional and shear travel time
for a specific case using the Biot equation.
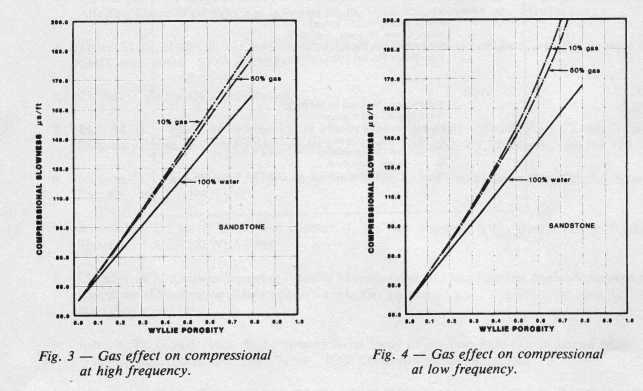
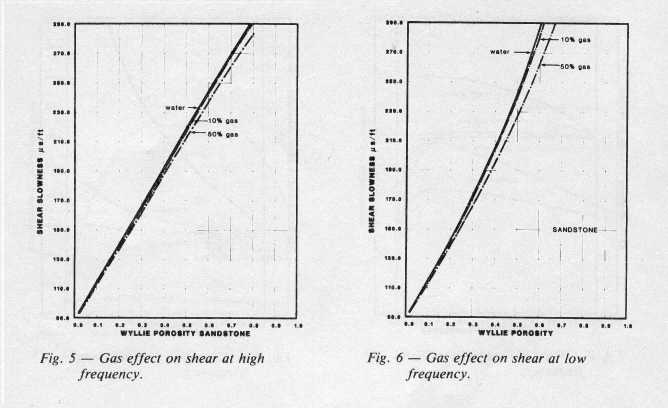
The plots below shows the effect of gas on compressional and shear
velocity for a typical rock sample at 6000 feet with 30 percent
porosity, calculated from the Biot equations. Notice that compressional velocity drops rapidly with
very small gas saturations, compared to the water filled case. Shear velocity increases very
slightly with gas and is therefore little affected. Poisson's
Ratio and velocity ratio Vp/Vs also decrease with small gas
saturations and then remain roughly constant regardless of
saturation.
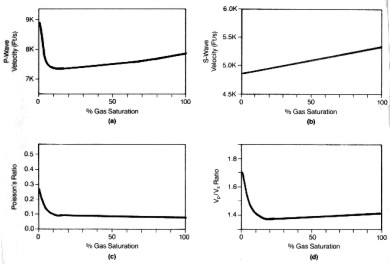
Effect of gas on compressional velocity (top
left), shear
velocity (top right), Poisson's Ratio
(bottom left), and Vp/Vs
ratio (bottom right) (Anderson 1984)
The
gas effect on compressional and shear travel time are given
below as a function of porosity. These charts can be used to estimate DELTmod for
most clean gas bearing rocks. These results underestimate the
gas effect when compared to the pseudo-travel time method, but
are probably more realistic in shallow to medium depths (3000 to
8000 feet). The effect
at low (seismic wavelet) frequency is much stronger than it is
for high (sonic log) frequencies.
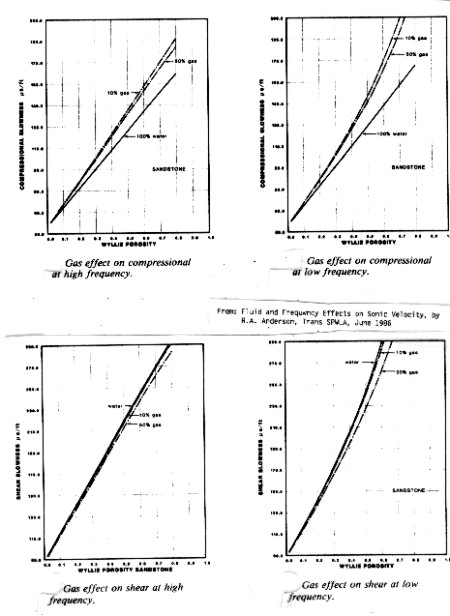
Gas effect at high (sonic log) and low
(seismic) frequencies - compressional wave travel time (upper)
and shear wave (lower)
In
the range of 5 to 30% porosity, all the lines can be
approximated by straight lines. By comparing the gas saturated
lines with the water saturated lines for the low frequency data, we obtain:
12: DTCmodgas = DTCmodwtr * (1 + 0.275 * PHIe)
13: DTSmodgas = DTSmodwtr * (1 + 0.237 * PHIe)
DTCmodwtr and DTSmodwtr are the compressional and shear travel
times for a water-filled reservoir. In water zones, these values
could be the actual log readings if there are no obvious borehole
effects. In gas zones, where the sonic log sees some residual gas,
the values are obtained from the response equation
described earlier, using log analysis results for porosity and
lithology, and SW = 1.00.
The
effect on the ratio of shear to compressional travel time (Vp/Vs
Ratio) is
shown below. The effect at low (seismic wavelet)
frequency is much stronger than it is for high (sonic log)
frequencies. Therefore, the low frequency data should be used in
modeling sonic log response so that it will match the seismic
impulse response.
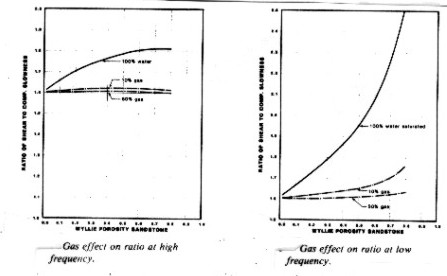
Gas effect at high (sonic log) and low
(seismic) frequencies - Vp/Vs Ratio is nearly constant for
gas
saturations above 0.10 but increases with porosity in water
saturated rock.
There is no shortage of alternative fluid replacement methods
published since our original work in 1979 and Anderson's in 1984: Castagna, Greenberg
and Castagna, Aki and Richards, Batzie and Wang, Toksoz et al,
Krist,
among others. Use caution when applying these alternate models;
for example Toksoz gets opposite results to Anderson when
computing gas bearing zones. Obviously, some parameters or
assumptions must be different.
|

