|
 Resistivity Concepts in Fractured Reservoirs
Resistivity Concepts in Fractured Reservoirs
The
following Sections deal with the dual porosity model as
defined by Dr Roberto Aquilera in his original paper,
“Analysis of naturally fractured reservoirs from
conventional well logs”, R. Aguilera, The Journal of
Canadian Petroleum Technology, p. 764-772, 1976. Recently Dr
Aquilera has published a triple porosity model and Dr Zoltan
Barlai has used a “five channel” porosity model with some
success, neither of which is discussed here. Dr Aquilera has
also published a hard cover textbook on the dual porosity
model and fractured reservoirs in general. Students should
review his material to augment the material presentrd ,
which is briefer than the original material.
There
Sections contains some amplified or re-defined terminology that
contrasts with some of Dr Aquilera’s definitions. Please be aware of
these differences when reading both works. Review the definitions
provided at the beginning of this Handbook before proceeding.
Quantitative analysis of fractured reservoirs is complicated by the
fact that other forms of porosity exist besides that contained by
the fractures. Thus a dual porosity model has been proposed to
account for both primary and secondary porosity. The theoretical
principles behind the dual porosity model have been published
previously in the literature by Aguilera and have been used by
others with some success in Mexico, Venezuela, the United States,
and Canada.
The term
"dual porosity" should not be confused with the "dual water" model
used for shaly formations. In addition, the fractured reservoir
literature uses the phrase "total porosity" to mean the sum of
effective matrix porosity plus effective fracture porosity. This is
very confusing as the phrase has a different meaning in the shaly
sand situation. Since there are fractured shaly reservoirs where the
distinction between total and effective porosity is important, we
will use the following definitions.
|
Effective
porosity
PHIe = PHIm +
PHIf
Total porosity
PHIt = PHIe +
Vsh * BVWSH |
Where:
PHIe = effective porosity
of dual porosity system (fractional)
PHIm = effective matrix
porosity in dual porosity system (fractional)
PHIf = effective fracture
porosity of dual porosity system (fractional)
PHIt = total porosity of
any rock (fractional)
Vsh = shale volume
(fractional)
BVWSH = bound water in
100% shale (fractional)
Some
fracture literature also uses the term secondary porosity to mean
fracture porosity, whereas this term has been used by others to
describe the porosity not seen by the sonic log, usually some
portion of the vuggy porosity. We prefer to use secondary porosity
in its geological sense and use the term fracture porosity in a
strictly literal sense.
To
develop the dual porosity model, we invoke the basic Archie
equations.
|
Archie’s
Laws
#1:
I
= RESD / (F * RW@FT)
#2: F = A / (PHIe ^ M)
Rearranged, these become the Pickett plot definition
In Water Zone ONLY
1: log(RESD) = - M * log(PHIe) + log(A*RW@FT)
2: M = (log(A*RW@FT) - log(RESD)) / log(PHIe)
In Flushed Zone ONLY
3: log(RESS) = - M * log(PHIe)+log(A*RMF@FT)
4: M = (log(A*RMF@FT) - log(RESS)) / log(PHIe) |
Where:
A = tortuosity exponent (unitless)
F = formation factor (unitless)
I
= resistivity index (unitless)
M = cementation exponent (unitless)
PHIe = effective porosity
of dual porosity system (fractional)
RESD = true )deep)
formation resistivity (ohm-m)
RW@FT = formation water
resistivity (ohm-m)
Analysis
of equations 2 and 4 indicates that a crossplot of porosity vs
resistivity on log-log coordinate paper will result in a straight
line with a slope of -M for zones of constant water resistivity (A *
RW@FT) and constant resistivity index (I).
A constant resistivity index implies that the zone has constant
water saturation (Sw), where Sw = (1 / I) ^ (1 / N). This plot has been called the Pickett plot and
is widely used to find both A * RW@FT and M for water zones and Sw
for hydrocarbon zones in conventional reservoirs.
IMPORTANT: This method is not suitable for shaly reservoirs as no
shale term is included in the Pickett plot. Therefore, be sure to
exclude shale or shaly zones from a Pickett plot.
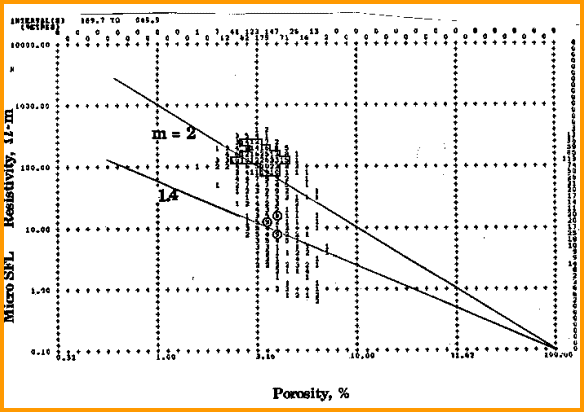
Porosity - resistivity crossplot (Pickett plot)
identifies M
For
reservoirs with fracture porosity, the value of M found from the
Pickett plot is smaller than the cementation exponent, M,
determined from a primary porosity sample in the laboratory, or
estimated from lithological descriptions, or from an
un-fractured portion of the reservoir. This is reasonable
because fracture porosity results in a reduction in tortuosity
and cementation. In addition, fractures can be invaded deeply by
drilling fluids, thus reducing RESD and the derived value of M
from the crossplot. The lower M may be compensating for invasion
as much as for the fractured nature of the rock. In any case, a
lower value for M decreases water saturation and this is needed
whether the lower resistivity is due to invasion or to lower
cementation.
Values
of M from the Pickett plot in the range 1.2 to 1.7 can be expected
for fractured reservoirs, as opposed to 1.8 to 2.4 for the
un-fractured portion of the same rock. The laboratory measurement of
M for a well-fractured rock is seldom successful, so there is not
much real data to use, except in competent samples with minor
micro-fractures.
We can
then redefine M to reflect these differences.
|
Definition
of Md and Mb
Md = cementation
exponent for dual porosity model, found from a Pickett plot
Mb = cementation
exponent for un-fractured matrix rock, found from laboratory
measurement, a Pickett plot in an un-fractured zone, or from
assumption based on lithology |
Choosing
Md and Mb
Normally, Md is chosen once for each fractured interval from the
Pickett plot, but there is no reason to believe it is a constant
because fracture intensity varies dramatically from foot to foot
within the reservoir. It is clear that every data point could have a
unique value of Md, assuming all are 100% wet.
A method
has been proposed by Rasmus whereby Md is calculated and used at
each level, thus providing a "variable M" method throughout the
zone. It is based on the sonic versus density neutron porosity:
|
Rasmus variable M
96: Md = log ((1 - (PHIe - PHIsc)) * (PHIsc ^ Mb) + (PHIe -
PHIsc)) / log PHIe
Thus for un-fractured rock:
97: log RESD = - Mb * log (PHIe) + log (A * RW@FT) + log (I)
And for fractured rock:
98: log RESD = -
Md * log (PHIe) + log (A * RW@FT) + log (I) |
The
derivation is rather lengthy and not shown here. A fracture
tortuosity term has also been omitted because it is often assumed to
be 1. This presumes that PHIe >= PHIsc and PHIsc has been adequately
corrected for lithology and shale. When there are no fractures,
PHIsc = PHIe and Md = Mb.
In many
cases, it is possible to carry out the evaluation by crossplotting (DELT
- DELTMA) vs RESD, or (DENS - DENSMA) vs RESD on log-log paper
instead of PHIe vs RESD. The sonic log method is not recommended if
vuggy porosity exists, because the sonic log does not see all this
porosity. Thus PHIsc will be too low and Md would be wrong.
Likewise, if PHIsc > PHIe, the method should be abandoned.
The
value of Md is determined by calculating the slope of the line drawn
through the south west points in the Pickett plot, which are assumed
to be water bearing levels. If no water bearing points are available
because there is no water zone in the fractured interval, it is
possible to make the plot by replacing RESD with RESS, the shallow
resistivity, based on the assumption that the invaded zone will be
more nearly 100% wet than the un-invaded zone. The constant in the
equation becomes (A * RMF@FT), but this value is known as well or
better than (A * RW@FT).
With the
value of Md determined from the crossplot or equation 96 and Mb
determined in the laboratory or estimated from lithology, it is
possible to complete the evaluation to quantify primary and fracture
porosities, as proposed by Aguilera.
|

