|
 Modeling the Sonic and Density Response From Regression
Modeling the Sonic and Density Response From Regression
Jay Patchett proposed a sonic editing technique in 1975 for
shales, based on the following:
1: log(COND) = A0 + A1
* log(DTC - 42)
+ A2 * log(CEC) + A3 * log(ES)
Where:
CEC = cation exchange
capacity of the shale
ES = effective stress (psi)
Since CEC is not readily available in most wells, this approach
was not terribly practical. However, by recognizing other work
that related CEC to gamma ray log response, the equation
becomes:
For
shale zones:
2: log(DTDsyn - 40) =
KW0 + KW1 * log(RSH)
+ KW2 * log(GR) + KW3 * log(ES)
A
similar equation for density is:
3: DENSsyn = KX0 + KX1
* GR + KX2 * DEPTH + KX3 * log (RSH)
For
sandstones:
4: DTCsyn = KY0 + KY1
* GR + KY2 * log(ES) + KY3 * PHIrs
5: DENSsyn = KZ0 + KZ1
* GR + KZ2 * DEPTH + KZ3 * PHIrs
Where:
PHIrs = porosity from the
shallow resistivity log
These models are decidedly not simple and a great deal of
calibration is required to make them work. Practitioners should
refer to the original paper for details of the method. In
addition, a sophisticated multiple linear regression program is
required.
 Case History
- Multiple Regression Editing
Case History
- Multiple Regression Editing
Here are three US examples from Patchett's work showing:
1. effect of sonic edits on synthetic
2. creation of synthetic sonic and density, with resulting synthetic
seismogram
3. comparison of regression derived synthetic with real data

Log editing by multiple regression - original and edited
logs and seismogram trace
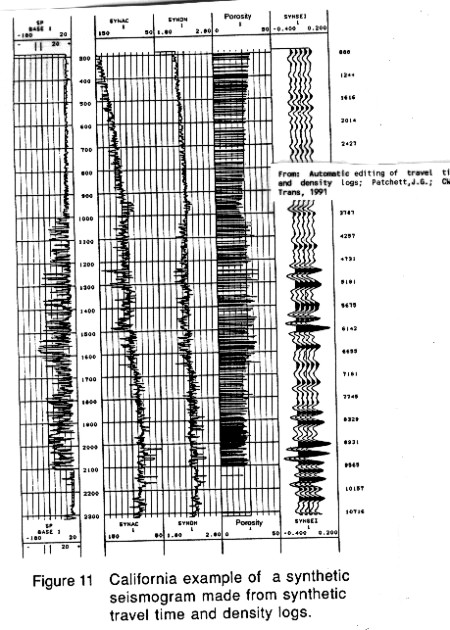
Synthetic sonic and density log from multiple regression

Comparison of synthetic to real seismic section
Other
examples are contained in the original paper and are well worth
reviewing. See "Automatic editing of travel time and density
logs", Patchett,J.G.; CWLS Trans, 1991.
|

