POROSITY BASICS
Porosity is the volume of the non-solid portion of the rock filled with fluids, divided by the total volume of the rock. Primary porosity is the porosity developed by the original sedimentation process by which the rock was created. In reports, it is often referred to in terms of percentages, while in calculations it is always a decimal fraction.

Secondary porosity is created by processes other than primary cementation and compaction of the sediments. An example of secondary porosity can be found in the solution of limestone or dolomite by ground waters, a process which creates vugs or caverns. Fracturing also creates secondary porosity. Dolomitization results in the shrinking of solid rock volume as the material transforms from calcite to dolomite, giving a corresponding increase in porosity.

Log analysts define porosity somewhat differently, due to the nature of the measuring techniques. These definitions are described later in this Chapter.

POROSITY IN SANDSTONES
We tend to think of sandstones as being composed of quartz grains, but this is a false impression based on too many idealized cinematic beaches and cast-away island songs. Most sandstones are made of many different minerals; some have no quartz at all. So in the following discussion, please think of sand grains as being composed of a variety of minerals, not necessarily pure quartz.

To acquire an appreciation for the values of porosity generally encountered, assume round balls of the same size are stacked on top of each other in columns. Calculations will show a porosity of 47.6%. Spherical sand grains 1/10 the size of the balls stacked one on top of the other will have the same porosity, 47.6%.

If the same balls are packed in the closest possible arrangement in which the upper ball sits in the valley between the four lower balls, the porosity is reduced to 25.9%. Again, changing the size of the balls will not change the porosity as long as all the balls are the same size.

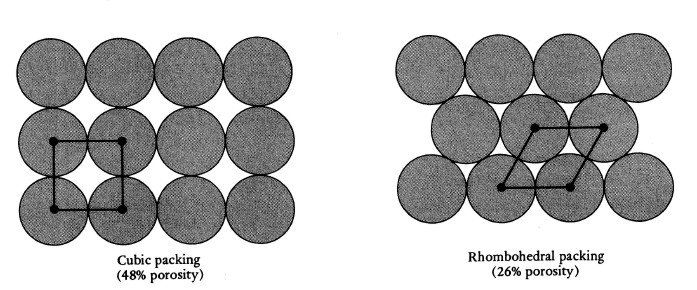
Cubic packing 47% porosity (left)   Rhombic packing 26% porosity (right)

Mixing the sizes of the balls will create lower porosity, since small ones can fit in spaces created between the larger ones. The term "sorting" is used to describe the distribution of grain sizes in a sandstone. Very well sorted rocks have fairly uniform grain size and high porosity. Poorly sorted sands have a wide range of grain size and poor porosity, illustrated below. Grain size classifications are shown on the scale at right, below.

Poorly Sorted                       Moderately Sorted                       Well Sorted                         Very Well Sorted
Low Porosity                          Poor Porosity                            Good Porosity                      Excellent Porosity

The highest porosity normally anticipated is 47.6%. A more probable porosity is in the mid-twenties. The normal range of porosities in granular systems is 5% to 35%.

In general, porosities tend to be lower in deeper and older rocks. This decrease in porosity is primarily due to overburden stresses on the rock, and cementation. There are many exceptions to this general trend, when normal overburden conditions do not prevail.

Shales closely follow the same porosity depth trend as sandstones. For example, in a recent mud the porosity may measure about 40%. It decreases rapidly with depth and overburden pressure until, at a depth of about 10,000 feet, normal porosities are less than 5%. Shales are plastic and therefore, compress more easily than sands.

These basic trends of porosity versus depth are not as noticeable in carbonates, where porosity is more a function of depositional environment and secondary processes, both unrelated to depth of burial.

Porosity in a real shale is not effective; that is, the water cannot move as quickly as in a sandstone with the same apparent porosity. Water in shale can be expelled over large geologic time periods, but it will not flow in the usual sense of the word.

However, many intervals that have been traditionally thought of as "shale" are really silty shales or sandy shales. These may have sufficient porosity to store hydrocarbons that might flow. This is especially true for gas, and many "gas shales" are silty shales with effective porosity. Other gas shales are mostly shale and gas is stored on the surface of kerogen within the shale. This is adsorbed gas.

Laminated shaly sands are also called gas shales in some literature. While they are definitely shaly and contain gas, the petrophysical model is quite different from gas shales or gas silts, so the "laminated" adjective should be retained.

Porosity in shaly sands varies with the amount and distribution of the clay minerals within the sandstone. The common distributions and their effect on porosity are shown below.

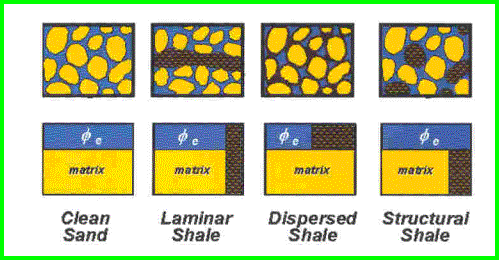
The Effect of Clay distribution on Porosity in a Shaly Sand. Sand grains are yellow, effective
 porosity is blue, and clay (including clay bound water) is coloured black.

For log analysis purposes, we define total porosity as the pore space (blue area in above illustration) plus the clay bound water (part of the black shading). Effective porosity is defined as the total porosity minus the clay bound water (blue area only). Further adjustments are sometimes made to generate useful or connected porosity, which excludes clay bound water and any unconnected pores, such as pin-point vugs or isolated pores inside the sand grains. 
 

POROSITY IN CARBONATES
Porosity in carbonates is more complicated than in sandstones, partly due to various classification methods and more combinations of carbonate fabric and associated porosity. Most of the porosity that is useful in carbonate reservoirs is secondary porosity, formed after deposition.

The use of the term, Secondary Porosity Index (SPI) by log analysts has led to much confusion. The term means the porosity defined by the difference between porosity derived from the sonic log and the primary porosity. The primary porosity is usually defined by core analysis or the density neutron log. Depending on the shape and size of the vugs, fractures, or caverns, the SPI may or may not be a good indication of secondary porosity.

Below are three different classification methods for carbonate porosity. Sample descriptions of the same rock will vary, depending on the wellsite geologist's age, training, and current knowledge of the geological literature. Dunham's method is the oldest and simplest, followed by Choquette's method, then by Lucia's, which is by far the most complex but most complete.

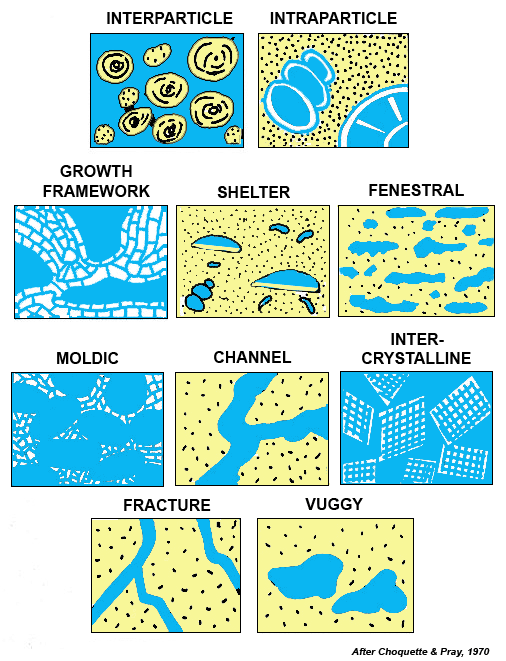
Porosity classifications vary according to the authority cited - this is Choquette's system
 and is widely used.

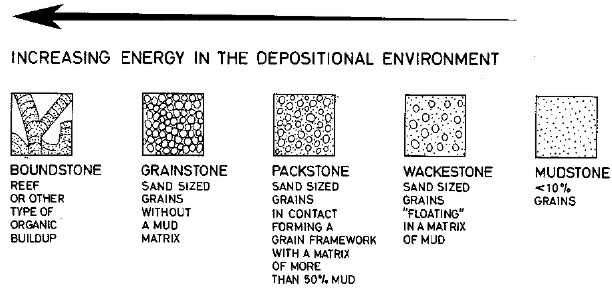
Dunham's classification of carbonate textures - these are independent of the porosity classification

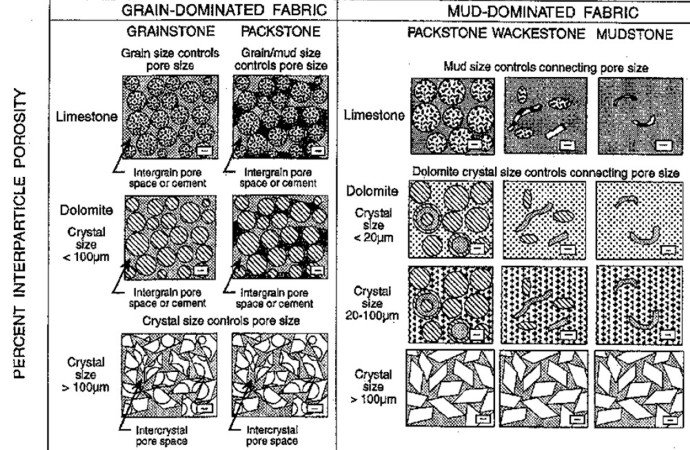
Lucia's classification of carbonates, expanding Dunham's classification to include porosity type

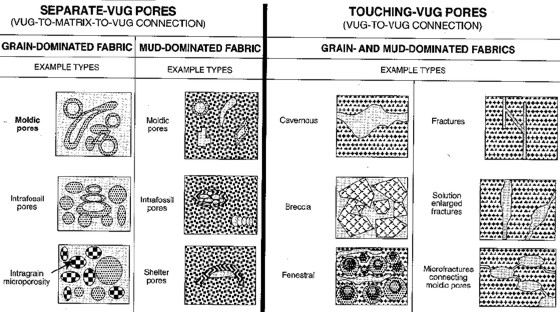
Lucia's classification extended to cover connected and unconnected vuggy porosity types

Useful Porosity
There is a recent trend among petrophysicists and engineers to partition porosity into a useful and a non-useful fraction. The concept of useful porosity, as opposed to effective porosity, is helpful where very small pores exist. These tiny pores do not connect to other pores and thus do not contribute to useful reservoir volume or reservoir energy. They are invariably water filled and nothing flows from them or through them. The tiny pores are called micro porosity; the larger, more effective, pores are called macro porosity. Personally, I prefer the term connected and unconnected (or poorly connected) porosity, as illustrated below:

Porosity definitions related to useful or connected porosity. Some micro porosity may not be observed in conventional core analysis. Most porosity indicating logs see unconnected porosity, but the sonic log may not see any or all of the microporosity.

Thus:
      1: PHIuse = PHIe - PHImicro

In sandstones, micro porosity is often associated with intraparticle porosity in volcanic rock fragments and kaolinite that are part of the sandstone mineral mixture. In carbonates, micro porosity is associated with micrite, matrix, fossil skeletons, or pin point vugs. Larger vugs are often connected.

The quantity of micro porosity cannot always be found directly from logs but is usually assessed as a constant fraction, KM1, of the effective porosity. This constant can be found by examination of thin section visual porosity. Where micro porosity is associated with silt or a volcanic mineral (Vmin2) in a quartz sandstone:
        2: KM1 = Vsilt / (Vqrtz + Vsilt)
OR 2A: KM1 = Vmin2 / (Vqrtz + Vmin2)
        3: PHIuse = PHIe * KM1

In some cases, the micro porosity is assumed to be a constant value instead of a constant fraction of the silt volume, PHIoffset, over an interval (ie, PHImicro is not proportional to effective porosity). This appears to happen in carbonates with unconnected pinpoint vugs (PHIppv), micritic carbonates (PHImict), or carbonates with matrix porosity (PHImatr). In all three cases, PHIoffset is found by comparing visual porosity in thin sections to log analysis porosity.
      4: PHIuse = PHIe - PHIoffset

In log analysis terminology, matrix porosity usually means effective porosity (PHIe). However, in petrographic (thin section) analysis, matrix porosity (PHImatr) is non-useful porosity contained in the very fine-grained matrix material deposited between the granular or crystalline rock structure.

PHIppv, PHImict, and PHImatr may be varied according to rules developed by the analyst for the zone. A crossplot of visual porosity from thin section analysis versus PHIe from logs is a useful tool for determining the appropriate correction to obtain PHIuse. Typical rules might be:

      5: PHIuse = PHIe - PHIsec
      6: PHIuse = PHIsec
      7: PHIuse = PHIe - KMATR * (1 - PHIe) / (1 - KMATR)
      8: PHIuse = PHIe - PHIsc * KMICT / PHISavg

KMATR and KMICT would be in the range 0.01 to 0.08, averaging 0.04, and cannot exceed PHIt.
 

Definitions of Porosity FOR LOG ANALYSIS PURPOSES
The above discussion covers the geological definitions of porosity. Petrophysicists, log analysts, and engineers use more specific terms based on the concept of total and effective porosity. Here are the definitions:

Non-useful porosity occurs as tiny pores that do not connect to any other pores. They are almost invariably filled with immoveable water and do not contribute to useful reservoir volume or energy. Such pores occur in silt, volcanic rock fragments in sandstones, and in micritic, vuggy, or skeletal carbonates. The NMR may see some of this non-useful porosity; the jury is still out.

 

POROSITY INDICATING LOGS
There are numerous porosity indicating logs, as shown in the box at right, and many flavours of each, depending on the age, design, and logging environment. Generic analysis equations, based on the Log Response Equation, for each basic tool type are contained in this Chapter. They will work for almost all available tool types. There may be rare occasions when a customized analysis model might be required.

All the porosity models require some assumptions about such things as fluid type and matrix rock properties. With the exception of the resistivity log formula, used for analysis of ancient logs, the methods involve corrections for the effects of shale.

Various methods are presented in other sections of this Handbook to calculate porosity from individual or combinations of two or more logs. Two-log combinations are termed crossplot methods, since the log data can be plotted on the X and Y axes of a graph. Three or more log combinations require solution by simultaneous equations, and are usually done on a computer.

Shale corrections are applied to porosity logs to determine effective porosity. Since shale contains some water, this water must be subtracted from the total porosity as measured by conventional logging tools. The mathematical method for finding shale volume is the same for all the shale distribution types, but the method for applying the shale correction to the porosity varies.

Correcting for shale is only half the battle. The other half is to correct for the mineral composition of the rocks. In most carbonate reservoirs, the lithology is usually reasonably well known from sample descriptions or can be determined from log response, so this step is relatively straightforward.

This is not true in sandstones because the mineral makeup of the sand is NOT usually described in much detail. There is a universal trend to give sandstones the physical properties of pure quartz, but this is almost universally NOT appropriate. Most sandstones contain other minerals besides quartz, such as mica, volcanic rock fragments, calcite, dolomite, anhydrite, and ferrous minerals, as well as the shale and clay described above. All of these minerals have different log responses than quartz. If a sandstone is assumed to be pure quartz when it is not, the commonly used properties of quartz will provide a pessimistic porosity answer.

Thus, authors and service company manuals that present quartz properties for “sandstone” are misleading their audience into believing these properties are constant. In more than 40 years of petrophysical analysis, I have never seen a thin section or XRD report that gave an assay of 100% quartz in any petroleum reservoir. A 100% quartz sand is very rare. If anyone doubts this statement, look at the PEF curve. If it reads more than 1.8, you have “quartz plus other things” in your sandstone.

There is a story (it may even be true) that reserves for the early North Sea discoveries were seriously underestimated because the mica in the sands was not accounted for properly. The engineers used density log porosity without correcting for the real matrix density. If true, good engineering practice would have undersized all the offshore equipment and early cash flow and rate of return on investment would have been significantly reduced. If the myth that sandstone is pure quartz is perpetuated, there will be more economic blunders of this type.

To further confuse the uninitiated, many logs show data on a "porosity" scale. These log curves are transforms of some measured physical property to an approximate porosity based on some arbitrary parameters. Examples are density, neutron, or sonic porosity on so-called Sandstone, Limestone, or Dolomite porosity scales. Porosity as defined by these transforms is only directly useful if there is no shale, the scale matches the rock mineralogy. and there are no accessory minerals. Real reservoirs are rarely this simple. DO NOT use these porosity transforms without further analysis unless all the arbitrary assumptions used to create them match exactly the rock you are analyzing.

Some people call these porosity curves an “interpretation”. They are not. They are merely a transform of the raw data to a more attractive scale. The difference between a transform and an interpretation is critical. Interpretation infers some intelligent thought went into creating and understanding the result. The service company running the log does not provide interpretations. YOU are the interpreter,

There are endless cases where a transform to an inappropriate porosity scale has caused millions in losses due to poorly informed analysts who see “gas cross over” when there is no gas, or who read porosity directly from the transform and either seriously over estimate or under estimate reservoir effective porosity.

In spite of these comments, a number of charts and tables in this Handbook show the word "sandstone' when they really should say "quartz". I have not edited the charts and tables taken from common sources, such as service company chart books, so the common usage of incorrect terminology is repeated even here.