|
 Calculating Overburden
Pressure
Calculating Overburden
Pressure
Overburden pressure is caused by the weight of the rocks above
the formation pressing down on the rocks below. This is sometimes
called overburden stress - stress and pressure have the same units
of measurement.
Integrating
the density log versus depth or estimating the average rock density
profile and integrating will calculate this pressure:
1. Po = KS9 * SUM (DENSi * INCR)
Where:
Po = overburden pressure (KPa or psi)
DENSi = density log reading at the i-th data point (kg/m3 or gm/cc)
INCR = digital data increment (meters or feet)
KS9 = 0.01 for metric units
KS9 = 0.0605 for English units
Overburden
pressure gradient is:
2: (Po/D) = Po / DEPTH
A
literature search will turn up some relationships for (PO/D) for
specific areas, such as this one for the North Sea:
3: (Po/D) = (ln(DEPTH - EKB) - 0.5185) / 3.47
In
this equation, depth is in meters.
NOTE: All depths must be true vertical depths.
|
Typical
values for (Po/D) |
psi/ft |
KPa/meter |
|
|
Sandstone
30% porosity |
0.91 |
20.6 |
|
|
Sandstone
20% porosity |
0.98 |
22.2 |
|
|
Sandstone
10% porosity |
1.05 |
23.8 |
|
|
Sandstone
0% porosity |
1.12 |
25.4 |
|
|
|
|
|
|
|
|
|
|
|
For
a real rock sequence, these values may be integrated over each
lithologic interval, or can be used to replace density log data
over bad hole or missing log intervals. If the density log is
in porosity units, use the appropriate transforms to build a
density log. The log below shows the type of editing that might be needed on
a density log before integration.
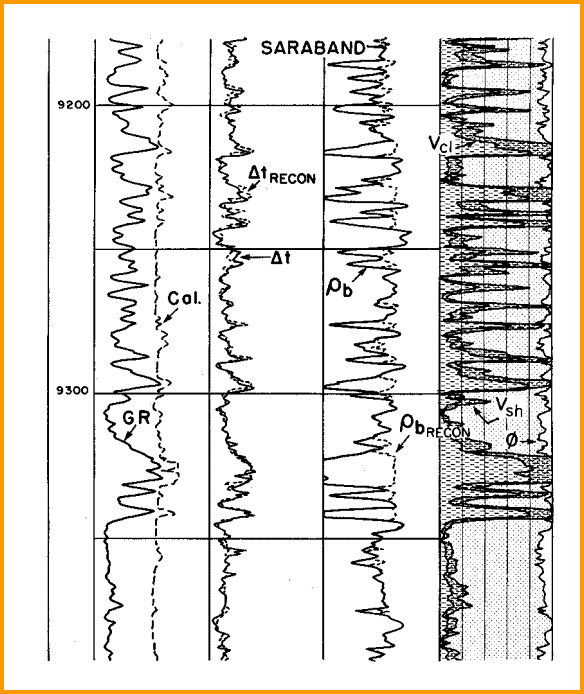
Editing density logs based on the log response equation
applied to a competent petrophysical
analysis of valid data.
 Calculating Normal Pore Pressure
Calculating Normal Pore Pressure
Normal pore pressures occur in many parts of the world. Normal
pressure gradients depend only on the density of the fluid in
the pores, integrated from surface to the depth of interest. Fresh
water with zero salinity will generate a pressure gradient of
0.433 psi/foot or 9.81 KPa/meter. Saturated salt water generates
a gradient of 0.460 psi/ft or 10.4 KPa/meter.
4: Pp = KP1 * DEPTH
5: Ps = KP2
Formation
pore pressure gradient is:
6: (Pp/D) = Pp / DEPTH
Where:
DEPTH = formation depth (ft or meters)
Pp = formation pressure (psi or KPa)
(Pp/D) = formation pressure gradient (psi/ft or KPa/meter)
Ps = surface pressure (psi or KPa)
KP1 = 0.433 to 0.460 psi/foot for English units
KP1 = 9.81 to 10.4 KPa/meter for Metric units
KP2 = 14.7 psi for English units
KP2 = 101 KPa for Metric units
NOTE:
All depths must be true vertical depths.
Formation
pore pressure (Pp) is the pore pressure used fracture pressure equations. The best source of pore pressure
data is the drill stem test (DST) or repeat formation tester (RFT)
extrapolated formation pressures from many zones in many wells,
plotted versus depth. Commercial databases containing this information
are available, or the data can be tabulated from well history
files.
The
slope (Pp/D) of a series of best fit straight lines drawn through
the data points will provide the pressure gradient required. The
hydrocarbon content will give lower gradients: oil gives a Pp/D
between 0.30 and 0.43 psi/ft (6.78 to 9.81 KPa/m). Gas zones will
have gradients from 0.05 to 0.30 psi/ft (2.26 to 6.78 KPa/m).
Partially depleted reservoirs may have abnormally low pore pressure
if there is no active aquifer, water injection, or gas injection
to support the reservoir pressure.
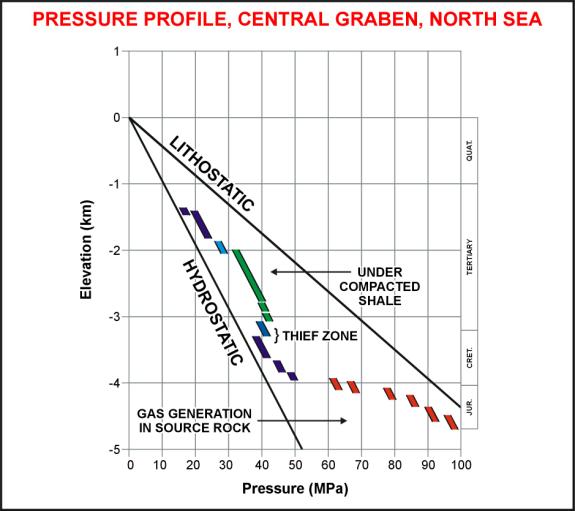
Pore pressure plot versus depth for North Sea - straight
line at left is normal pore pressure, line at right is
overburden pressure, dots are measured pore pressure.
Some
engineering problems require the initial formation pressure, before
any production has occurred. The pore pressure needed for fracture
pressure calculations is the current pore pressure at the time
the frac is to be performed. Since reservoir pressure depends
on the past history of production from all wells in the pool,
local pressure anomalies may be present. The best pressure to
use is the actual, measured, extrapolated shut in pressure for
the zone and well to be fractured.
If
no measured formation pressures exist, the mud weight hydrostatic
pressure can be taken as the upper limit for the pore pressure.
A lower limit would be the mud weight during a gas kick.
 Identifying Abnormal Pore Pressure
Identifying Abnormal Pore Pressure
In general, sonic and density logs in shales show trends versus
depth due to compaction. Trend lines drawn over the shale
intervals will follow the log curves in normal pressure. Sonic
and density log curves will depart to the left of the trend
lines in over-pressured shales. Neutron and resistivity logs may
also show departures to the left of their trend lines, but are
usually less sensitive than sonic and density.
Reservoirs
surrounded by these over-pressured shales will also be
over-pressured and may cause drilling difficulties or gas kicks into
the mud system. At worst, a well blowout may occur. To reduce this
risk, it is prudent to review sonic and density logs from offset
wells to locate the top of over-pressured zones and use this
knowledge to plan drilling and mud programs.
Seismic inversion
of vertical seismic profiles can also be used. These are very
valuable in the current drilling well since the technique can see a
considerable distance below the drill bit. This allows the operator
to finetune the estimated depth to top of over-pressure that had
been determined earlier from offset wells.
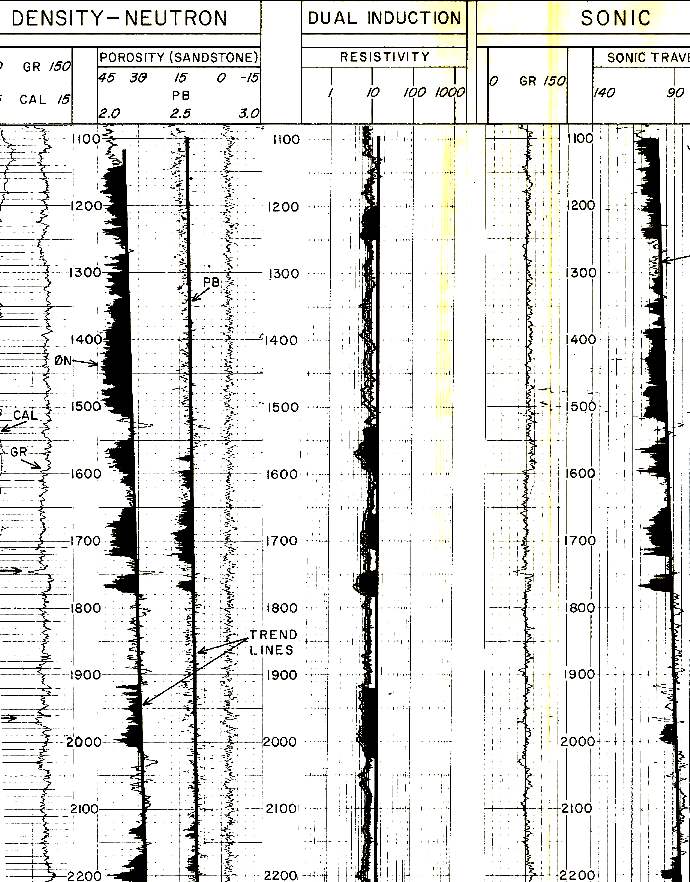
Example of trend lines in a slightly over-pressured shale. Gas kicks
occured between 1900 and 2000 feet.
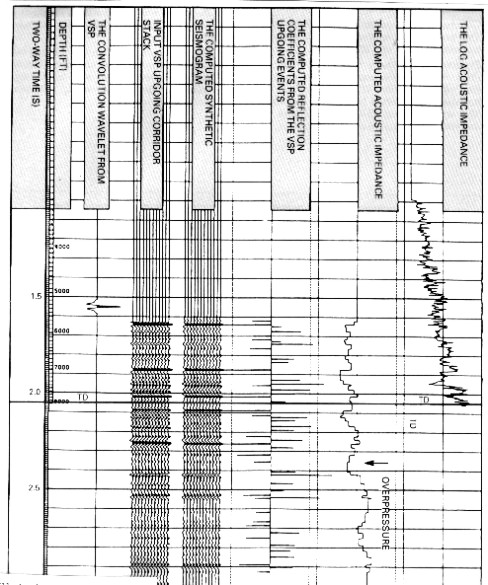
VSP, synthetic seismogram, inverted VSP, and
original sonic log. Arrow shows overpressure zone on inverted
VSP below current drill depth, indicated by base of sonic
log on far right.
 Calculating Abnormal Pore Pressure
Calculating Abnormal Pore Pressure
In some
reservoirs, pore pressure is higher than normal. These
are called overpressured or abnormal pressured zones. The best
source of pore pressure is still the extrapolated formation pressures
derived from DST or RFT data.
Some
gas sands are naturally underpressured due to burial at depth
with subsequent formation expansion after surface erosion. There
is also some suspicion that glaciation may have pressured then
relaxed these zones. Measured pressures are the only source of
pressure data for such zones.
Where
overpressure data is sparse, a log analysis technique is sometimes
helpful. It relies on fitting lines to semi-log plots of sonic
travel time in shale versus depth.
First,
we need to run a simplified log analysis, just to see where the
shales are:
7: Vsh = MIN(1,MAX(0,((GR - GR0) / (GR100 - GR0))))
8: PHIe = MIN(PHIMAX*(1 - VSH),MAX(0,0.5 * (PHIN - Vsh * PHINSH +
PHID - Vsh * PHIDSH)))
You
can substitute a more sophisticated log analysis model if desired.
It is used for displaying shale, porosity, and lithology on the
depth plot to aid in choosing the normal shale trend line on the
sonic log.
Find
DTCsh points for the depth plot:
9: IF Vsh > 0.5 THEN DTCsh = DTC OTHERWISE DTCsh = 0
Fit
a best fit or eyeball line to the DTCsh data points (ignoring
all zero or null data) above the overpressure zone - this is the
normal pressure trend line:
10: DTCnorm = 10^(log(DTCsh1) - ((DEPTH / DEPTH1) * (log(DTCsh1) - log(DTCsh0))))
11: DTCdiff = MAX (0,DTCsh - DTCnorm)
Where:
DTCsh0
= DTCnorm at zero depth
DTCsh1 = DTCnorm at DEPTH1
on the best fit trend line.
The best fit line through the shale DTC data points define
DTCnorm. Equation 10 is an example of such a best fit line. It
uses DTCsh0 and DTCsh1 to define the slope of the line. In the
example log plot shown a little lower down on this page, DTCnorm
is the straight line (on a logarithmic DTC scale) on the left
edge of the black shading in the DTC track. The right-hand edge
of the black shading is the actual DTC, showing a departure from
the trend line towards higher DTC values, thus indicating
overpressure.
In equation 10,
DTCsh0 is the extrapolation of the DTCnorm line to zero depth,
about 550 - 600 usec/m in this exampl;e. DTCsh1 is picked from the
DTCnorm line at DEPTH1, usually at the deepest depth where shale
exists in the wellbore.
Calculate
overburden pressure gradient from an area specific transform or
by integrating the density log:
12: (Po/D) = (ln (DEPTH - EKB) - 0.5185) / 3.47
13: Po = (Po/D) * DEPTH
NOTE:
All depths must be true vertical depths.
Calculate
pore pressure gradient:
14: (Pp/D) = (Po/D) - ((Po/D) - 1) * (MIN (1 , DTCnorm / DTC))^3
15: Pp = (Pp/D) * DEPTH
This
equation is very sensitive to the choice of the normal trend line.
The exponent 3 in the equation may also need adjustment.
 CONVERting Pressure TO A
"HEAD OF WATER"
CONVERting Pressure TO A
"HEAD OF WATER"
Expressed
as a “head of water” in meters for hydrodynamic maps:
16: HEADp = ((Pp/D) - 1) * (DEPTH - EKB)
To
convert DST or RFT data to a head of water, rearrange equation
16 to read:
17: HEADrft = MAX(0,-DEPTH + EKB + RFTPRES / 9.81)
The
Pp values from log analysis can be compared to DST or RFT pressures
and adjustments made to the best fit lines if needed. There is
no good reason to believe that the pressure in a reservoir will
be equal to the pressure in the shale above it. However, if a
calculated Pp in a shale is less than a measured Pp in a deeper
reservoir, then we would expect the formation to leak hydrocarbons
or water upward into shallower formations, or even to the surface.
To
convert DST or RFT data to a head of water, rearrange equation
10 to read:
17: HEADrft = MAX(0,-DEPTH + EKB + RFTPRES / 9.81)
 EXAMPLE OF
OVERPRESSURE LOG ANALYSIS
EXAMPLE OF
OVERPRESSURE LOG ANALYSIS
An
example of this technique is illustrated below.
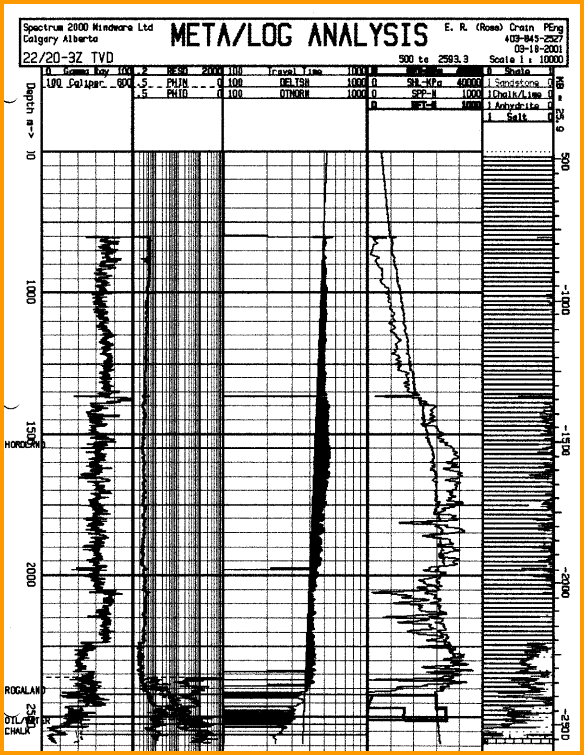
Overpressure log analysis plot versus depth. Black shading
in sonic track indicates overpressure interval. Note that sonic
scale is logarithmic and in reverse direction compared to a
normal log, and at a highly compressed vertical scale.
|

