|
 Fracture Pressure BASICS
Fracture Pressure BASICS
A major use of
mechanical properties from log analysis is in the design of casing
and mud weight programs for new wells to minimize the chance for
accidental formation breakdown and loss of circulation while
drilling. The critical pressure for formation breakdown in open hole
is called the “fracture pressure”.
A second use is
in the design of hydraulic fracture treatments to improve oil or gas
well performance. The critical pressure in such a design is the
“minimum horizontal stress”. Hydraulic fractures are usually
performed through perforations in well cemented casing. The pressure
required to break a rock in this scenario is lower than in open
hole. Unfortunately, this is often called the “fracture pressure” in
much of the literature, and can easily be confused with the fracture
pressure calculated for open hole situations.
Hydraulic
fracturing is a process in which pressure is applied to a reservoir
rock on purpose in order to break or crack it. These cracks are
called hydraulic fractures. Most hydraulic and natural fractures are
near vertical and increase well productivity significantly.
Hydraulic
fracturing may use sand to prop the fracture open, so it cannot
re-seal itself due to the enormous pressure exerted by the overlying
rock. Some reservoirs have natural fractures; others need to have
fractures added by us. Some wells flow oil and gas at rates that
make fracturing unnecessary.
Fracture
optimization involves designing a fracturing operation that is
strong enough to penetrate the reservoir rock and yet weak enough
not to break into zones where it is not wanted. In addition, a cost
effective design that minimizes time and materials is needed.
The extent of a
hydraulic fracture is a complex relationship between the strength of
the rock and the pressure difference between the rock and the
fracturing pressure. The extent is defined by the fracture
dimensions - height, depth of penetration (wing length or fracture
length), and aperture (width or opening).
One measure of a
rock's strength is Poisson's Ratio. Poisson's Ratio are low (0.10 to
0.30) for most sandstones and carbonates. These rocks fracture
relatively easily. Poisson's Ratio is high (0.35 to 0.45) for shale,
very shaly sandstone, and coal. These rocks are more elastic and are
harder to fracture. Shales are often the upper and lower barrier to
the height of a fracture in conventional sandstone.
A useful
indicator of rock strength is the Fracture Toughness Modulus,
defined as:
1: FTM = ((PR / (1-PR))^2) / N
Shales have a higher FTM than most reservoir rocks.
The lateral extent
of a fracture is primarily determined by Young's Modulus. Stiffer
rocks have higher Young's Modulus and are easier to fracture.
By using
radioactive tracers in the fracturing fluid, the extent of the
fracture can be traced by a gamma ray log. Adequate fracture depth
of penetration (fracture length) is also desired, as is fracture
aperture (fracture width). These are not as easy to determine from
logs as is the fracture height. Different tracer elements are used
during the frac so that a spectral gamma ray log can be used to
determine depth of penetration.
Fracture
pressure is the pressure needed to create a fracture in a rock while
drilling in open hole. Closure stress is the pressure needed to
fracture a rock through perforations in cased hole. In some
literature, closure stress and fracture pressure are used
interchangeably or ambiguously.
Both are
determined by the overburden pressure (a function of depth and rock
density), pore pressure, Poisson's Ratio, porosity, tectonic
stresses, and anisotropy. Breakdown pressure is the sum of the
closure stress and the friction effects of the frac fluid being
delivered to the formation. Breakdown pressure can be considerably
higher than closure stress.
Closure
stress is the pressure at which the fracture closes after the
fracturing pressure is relaxed. It is usually between 80 and 90% of
breakdown pressure. Rocks with high closure stress are harder to
frac (take more horsepower) than the same rocks with lower closure
stress. Shallow shaly sands have high closure stress because they
have high Poisson's Ratio.
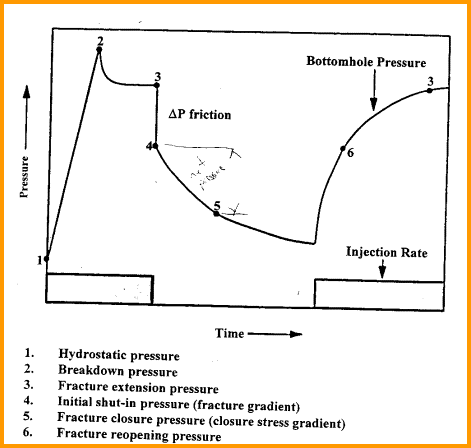
Mini-frac (cased hole) or leak-off test (open hole) pressure
test versus time, showing
definitions of pressure terminology
Many
technical papers and computer programs use pressure gradients
instead of pressures to define the calculations. Typical pressure
gradient values are:
Pore
pressure - normal pressure regime
KP1 = 0.433 to 0.460 psi/foot for English units
KP1 = 9.81 to 10.4 KPa/meter for Metric units
Pore
pressure - abnormal pressure regime
KP1 = 0.460 to 1.00 psi/foot for English units
KP1 = 10.4 to 22.6 KPa/meter for Metric units
Overburden
pressure
KP1 = 0.91 to 1.26 psi/foot for English units
KP1 = 20.6 to 28.5 KPa/meter for Metric units
Closure
stress - typical range
KP1 = 0.63 to 0.88 psi/foot for English units
KP1 = 12.0 to 20.0 KPa/meter for Metric units
The
average closure stress in the undisturbed part of the Western
Canadian basin is 16.5 KPa/meter.
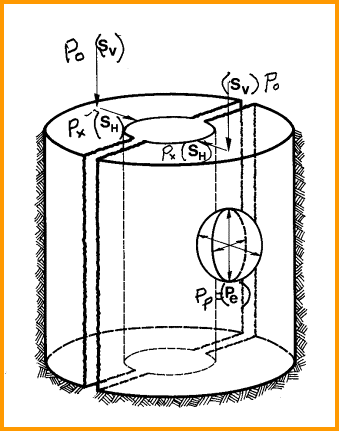 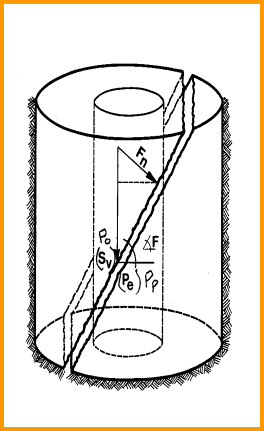
Stress regime - no tectonic stress (left), tectonic stress (right)
 CALCULATING
CLOSURE and FRACTURE
STRESS CALCULATING
CLOSURE and FRACTURE
STRESS
 CASE
1: Isotropic Reservoir (Basic Model)
CASE
1: Isotropic Reservoir (Basic Model)
The stress equations are:
1: KPR1
= PR / (1 – PR)
2: Px = Py = KPR1 * Po + (1 – KPR1) * Pp * ALPHA
3: Pclos = Py
4: Pfrac = 2 * Px
NUMERICAL EXAMPLE:
1.
Typical overpressure case:
Assume PR = 0.20 so KPR1 = 0.25
Assume Po = 1000 psi, Pp = 8000 psi
Assume Porosity = 0.20 so ALPHA = 0.62 + 0.935 * Porosity = 0.80
Pclos = 0.25 * 10000 + .0.75 * 8000 * 0.80
= 2500 + 6000 * 0.80
= 2500 + 4800 = 7300 psi
So closure stress in this example is less than pore pressure. If
porosity were higher, Biot’s constant ALPHA would be closer to 1.0
and closure stress would be greater than pore pressure.
2.
For a tyouxak normal pressure case:
Assume Pp = 4500 instead of 8000 psi
Pclos = 0.25 * 10000 + .0.75 * 4500 * 0.80
= 2500 + 3400 * 0.80
= 2500 + 2700 = 5200 psi
So closure stress is more than pore pressure.
If PR = 0.20 and porosity = 0.00, then ALPHA = 0.00, Pp = 0.0, and
Pclos = 2500, a very counter intuitive result.
Values have been rounded for demonstrarion purposes.
To initiate a frac, you only need to exceed closure stress.
 CASE
2: Anisotropic Reservoir (Standard Model)
CASE
2: Anisotropic Reservoir (Standard Model)
The stress equations are:
1:
KPR1 = PR / (1 – PR)
2: Px = KPR1 * Po + (1 – KPR1) * Pp * ALPHA + Pext
3: Py = KPR1 * Po + (1 – KPR1) * Pp * ALPHA
4: Pclos = Py
5: Pfrac = 3 *
Px – Py + Ts
 CASE
3: Anisotropic Reservoir (Iverson Model)
CASE
3: Anisotropic Reservoir (Iverson Model)
The stress equations are:
0: KPR1 = (PRyz * PRxy + PRxz) / (1 - PRxy * PRyx)
Assume PRxy = PRxz = PRmax
And PRyx = PRyz = PRmin
Then 1: KPR1
= (PRmin * PRmax + PRmax) / (1 - PRmax * PRmin)
2: Pclos = KPR1 * Po + (1 – KPR1) * Pp * ALPHA + Pext
 CASE
4: Anisotropic Fractured Reservoir (Iverson Model)
CASE
4: Anisotropic Fractured Reservoir (Iverson Model)
The stress equations are:
0: KPR1 = (PRy^2 + PRx) / (1 - PRy^2)
Assume PRy = PRmax
And PRx = PRmin
Then 1: KPR1
= (PRmin * PRmax + PRmax) / (1 - PRmax * PRmin)
2: Pclos = KPR1 * Po + (1 – KPR1) * Pp * ALPHA + Pext
 CASE
5: Total Stress Equation (Barree Model)
CASE
5: Total Stress Equation (Barree Model)
1:
KPR1 = PR / (1 – PR)
2: Pclos = KPR1 * (Po - ALPHAv * (Pp + Poff)) + ALPHAh
* (Pp + Poff) + Y * STh + Pext
The
usual assumption is that ALPHAv = ALPHA and ALPHAh = 1.00. Poff
accounts for pressure decline in the reservoir due to depletion
from offset wells. STRh and Pext are still assumptions and are
found by calibration to mini-fracs.
Where:
Px = stress in the maximum stress direction (psi or KPa)
Py = stress in the minimum stress direction (psi or KPa)
Po = overburden pressure (psi or KPa)
Pp = formation (pore) pressure (psi or KPa)
PR = Poisson’s ratio (fractional)
PRmax = Poisson’s ratio calculated with minimum DTS (fractional)
PRmin = Poisson’s ratio calculated with maximum DTS (fractional)
ALPHA = Biot’s elastic constant (fractional)
ALPHAh = horizontal Biot’s elastic constant (fractional)
ALPHAv = vertical Biot’s elastic constant (fractional)
Pext = unbalanced tectonic stress (psi or KPa)
STRt = tensile strength (psi or KPa)
Pclos =
formation closure stress in cased hole (psi or KPa)
Pfrac = formation fracture pressure (psi or KPa)
(Pf/D) = fracture pressure gradient (psi/ft or KPa/meter)
Y = Young's Modulus (psi)
STRh = regional horizontal strain (microstrains)
Poff = Pore pressure offset (psi)
When
formation stress is isotropic (equal in all directions),
the tectonic stress (Pext) is zero and Px equals Py.
Some previous authors have ignored Biot’s Constant
ALPHA in their equations. Since ALPHA = 1.0 only rarely,
leaving ALPHA out of the equation is not a good idea for
real rocks when the zone is porous. Tensile strength (Ts)
of most rocks is low or zero so the term is usually ignored.
In all the above cases, the fracture pressure for a zero
porosity case can be calculated by setting ALPHA = 0 and
PR = PRo. When ALPHA = 0, there is no contribution from Pp
(pore pressure) as there are no pores to transmit this pressure
against the frac fluid.
If
crossed dipole sonic data is available, anisotropic stress can
be noticed by differences in the X and Y axis displays of both
the compressional and shear travel times. When this occurs, all
the elastic constants can be computed for both the minimum and
maximum stress directions. This requires the original log to be
correctly oriented with directional information, and may require
extra processing in the service company computer center.
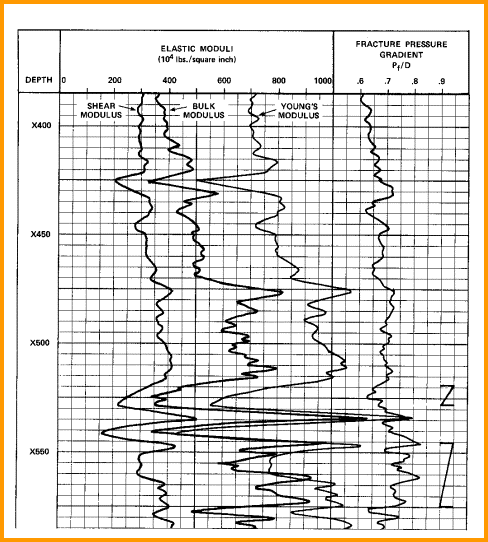
Sample fracture pressure gradient log
 Calibrating Fracture Pressure Gradient
Calibrating Fracture Pressure Gradient
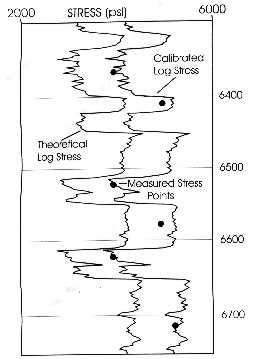 Because
so many assumptions are made in computing elastic constants and
pressure gradients, calibration is essential. If all the corrections
for frequency, gas, dynamic to static, anisotropy, and so on are
performed first, the correction factors may be relatively small.
The cause for error may even become apparent and the correction
might be made to Poisson's Ratio or overburden pressure. However,
the more usual case is that the cause is unknown. Because
so many assumptions are made in computing elastic constants and
pressure gradients, calibration is essential. If all the corrections
for frequency, gas, dynamic to static, anisotropy, and so on are
performed first, the correction factors may be relatively small.
The cause for error may even become apparent and the correction
might be made to Poisson's Ratio or overburden pressure. However,
the more usual case is that the cause is unknown.
A
common correction method is to compare log analysis stress profiles
with individual results from single or multiple mini-fracs. The
correction may be a linear shift of the log derived curve, such
as the example in the log at the right.
Mini-fracs
or leak-off tests should be run to verify that the computed fracture
pressure is close to the leak-off pressure. These tests are also
called pump-in tests. If they are not equal, then
there is anisotropy or tectonic stress (Pext). Alternatively,
some of the data or assumptions that went into calculating Po,
Pp, Pfrac, PR, or ALPHA might be wrong. The math should be iterated
to obtain a good match to the mini-frac without resorting to unreasonable
gradients or rock properties.

Leak-off pressure test versus time
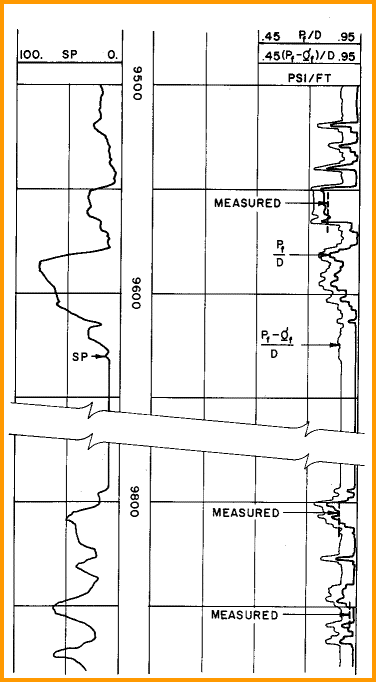
Fracture pressure gradient log showing shift to match
measured
closure stress (black dots).
An
alternative fracture pressure approach ignores all the log derived
data. Since the calculation must be calibrated anyway, why not
calibrate directly to available mini-fracs, and ignore the log
data? Mike Cleary proposed the following equation:
19: Pfrac = A * Po + B * Pp + C
Where:
A, B, C are constants derived from regression with pressures from
mini-fracs.
This
approach only works when sufficient tests exist over a moderate
depth range. It is of course useless where there is no test data.
It also loses a lot in translation, since the underlying physics
is hidden from view.
Because
of the major improvements in measuring shear sonic travel time
that have occurred in the last 10 years or so, and the recognition
and measurement of anisotropy in acoustic properties, many of
Cleary's complaints about elastic properties from acoustics have
disappeared. His ABC method may not need to be invoked as often
as in the past.
My
advice is try the log analysis method first if decent modern data
is available. Calibrate results to mini-fracs. Try and find the
sources of errors and fix them. When there is no decent log data,
use Cleary's ABC approach.
 Calculating Fracture Extent
Calculating Fracture Extent
Programs for fracture design are commonly called "frac height"
programs, but fracture extent (width) and fracture aperture are
also vital results. The math for this software is a little complicated
for this Chapter, and we assume you have a commercial software
product to perform the work. Accurate elastic constants and pressure
values derived as in previous Sections will be needed, and calibration
will still be required.
The modern use of the elastic properties and fracture pressure
gradient data in the computer creates some very impressive colour
displays to present the hydraulic fracture design to potential
customers. The same data can be entered into 3-D
modeling programs and compared to real frac jobs to assist in
frac job optimization.
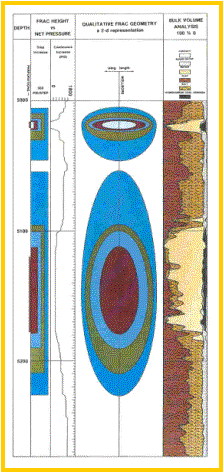 FracHite log (left)
FracHite log (left)
|
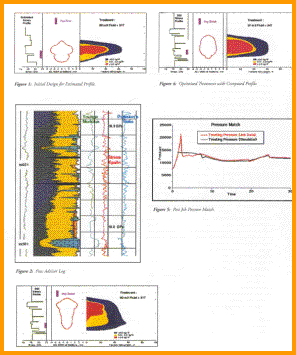 Fracture optimization model
Fracture optimization model
|
 Gamma Ray Logging to Confirm Fracture Placement
Gamma Ray Logging to Confirm Fracture Placement
To determine where a hydraulic fracture really goes into a formation,
some of the propping material can be coated with radioactive tracer
materials. After the fracture stimulation treatment is finished,
a standard gamma ray log is run to locate the tracer elements.
A base log must be run before the fracture stimulation to make
comparison easy.
The
fracture height determined from observation of the gamma ray log
is used in type-curve-fit or simulation software, with the treatment
placement pressure curve, to calculate fracture length (depth
of penetration). The fluid plus proppant volume is used in the
simulation to calculate fracture width (aperture).
Some
fracturing companies use a spectral gamma ray logging tool to
locate different radioactive tracer elements that have been applied
to different sized propping materials. The finer sized proppants
will show the deepest penetration, with coarser material being
deposited closer to the wellbore. The spectralog gives a 3-D image
of the fracture length, height, and width (aperture). These tracers
have very short half-lives (hours or days) so no permanent radioactive
signature is created).
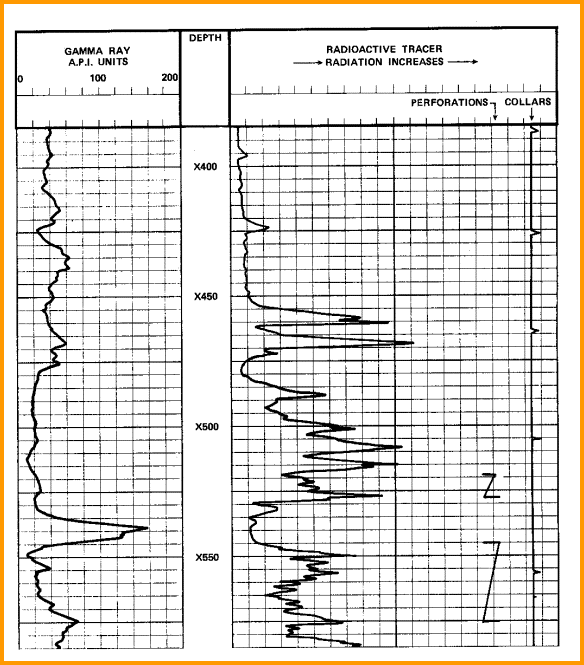
Post-frac radioactive tracer log with natural gamma ray in
Track 1 recorded before stimulation. Tracer log in Tracks 2 and
3 shows some placement into both sets of pwefs, but alsp above
upper perfs, possibly due to channel in cement behind casing.
The
gamma ray curve amplitude is a qualitative indicator of fracture
width (a
perture) since the quantity of radioactivity is proportional
to the volume of proppant that carries the tracer elements.
Note
that after a period of production from any reservoir, there may
be a permanent radioactive anomaly caused by precipitation of
uranium salts. A gamma ray log run in this situation helps to
identify where fluid flow is occurring. Some remedial action may
be possible if flow is not as expected. Some naturally fractured
reservoirs show this anomaly before production. In this case,
the precipitation occurred during migration of the hydrocarbon.
If
a producing or naturally fractured reservoir is to be hydraulically
fractured, a baseline gamma ray log should be run before the job.
The post-frac tracer log should be compared to this baseline,
rather than the original open hole gamma ray log.
 Determining Fracture Orientation
Determining Fracture Orientation
As mentioned above, when formation pressure is isotropic (equal
in all directions), the tectonic stress is zero and Pfrx equals
Pfry. In this situation, the borehole is round and spalling of
the formation is either non-existent or equal in all directions.
In stressed regions, such as in the Rocky Mountains, the borehole
will erode to an oval shape. The minimum diameter shows the direction
of maximum stress and the maximum diameter shows the direction
of minimum stress..
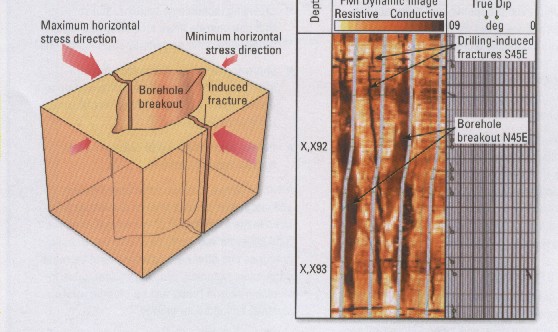
Borehole shape indicates stress direction –
maximum stress in direction of minimum hole
diameter. Formation microscanner and dipmeters have oriented caliper data.
Many
modern logs have an X and Y axis caliper, but not all of them
are oriented to true north. When directional data is recorded,
as with dipmeters and many modern resistivity tools, the X and
Y orientations are known, Statistical plots are helpful in choosing
the dominant direction).
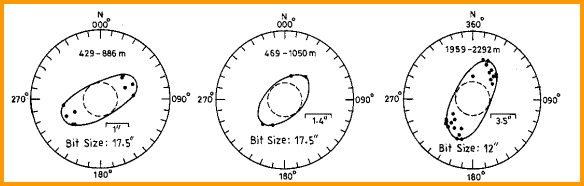
Borehole diameter indicates stress direction -
this example is from India where the minimum
stress direction
is NE - SW.
 A
hydraulic fracture will usually penetrate the formation in a plane
normal to minimum stress, or parallel to the plane of maximum
stress. Any stress anisotropy (tectonic stress) will cause the
fracture to be other than vertical. A
hydraulic fracture will usually penetrate the formation in a plane
normal to minimum stress, or parallel to the plane of maximum
stress. Any stress anisotropy (tectonic stress) will cause the
fracture to be other than vertical.
Natural
fractures take the same directions as hydraulic fractures, indicated
again by the borehole shape. In addition, the high angle dips
seen on an open hole dipmeter or image log, will also indicate this preferential
direction. Since most hydraulic fracture jobs are run in casing,
it is not possible to run a dipmeter or caliper survey to find
the orientation of a hydraulic fracture. The preferential direction
can be predicted from previous open hole data. Dipmeter and caliper
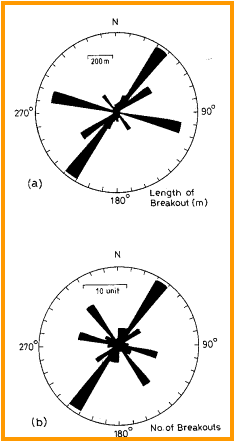
data can be displayed on rose diagrams to illustrate preferential
directions.
If
an azimuthal gamma ray log existed, the fracture orientation could
be located by a tracer survey. I am not aware that such a tool
exists, but it would not be difficult to design one..
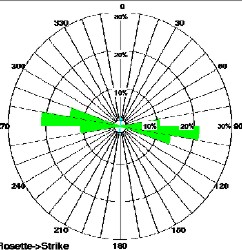
 Azimuth frequency (rose diagram) plots show direction of
dips seen on dipmeter and image logs. When steep dips caused by
fractures are isolated from lower angle bedding dips, the
direction of maximum stress xan be determined. In this case, the
direction is N30E. Azimuth frequency (rose diagram) plots show direction of
dips seen on dipmeter and image logs. When steep dips caused by
fractures are isolated from lower angle bedding dips, the
direction of maximum stress xan be determined. In this case, the
direction is N30E.
Stress
direction is not constant over geological time scales. Differences
in the direction of induced fractures (present day stress
direction), open fractures (some time ago), healed fractures (older
than open fractures), and small faults (could be any age) will help
to show the stress history of a region. An example log and rose
diagrams are shown below.
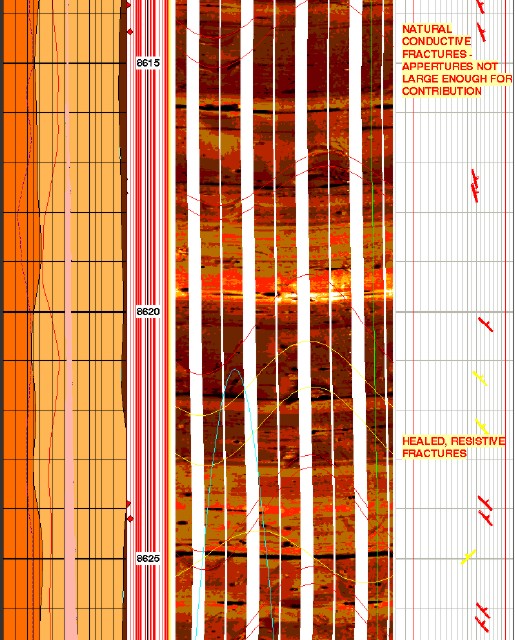
Image log in fractured reservoir: gamma ray (left track, shaded
red), image track (middle) with open fractures (red sine waves and
healed fractures (yellow sine waves), dip track (right) shows red
amd yellow dip angle and azimuth. There are no induced fractures in
this short interval. Bedding planes are near horizontal. Imagine
trying to locate these steep dips without the aid of a computer.
.
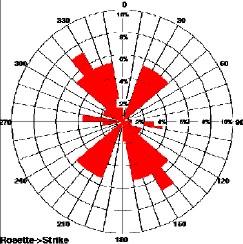
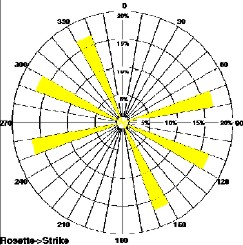
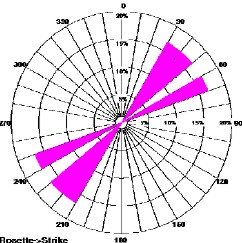
Induced fractures (top left) show current stress direction. Open
fractures (top right) show stress direction when fractures were
created, healed fractures (lower left) show different direction at
an earlier phase in geological time, and micro faults (lower right)
shows another stress regime was present when the faults occurred.
The
newest dipole shear sonic log is also an azimuthal tool with dipole
sources set at 90 degrees to each other. The example below shows the shear images for the X and Y directions. This
log can be run in open or cased hole.
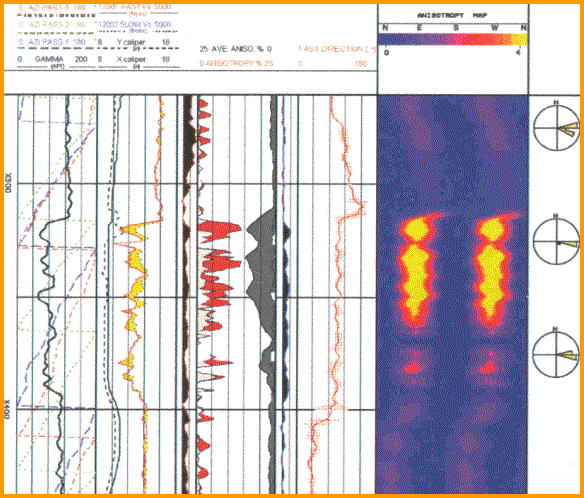
Dipole shear image log shows directional stress
- the Fast Direction is centered on
90 degrees (east - west) which
is also the maximum stress direction.
Resistivity and acoustic image logs also provide assistance in locating fracture orientation before the well
is cased.
|

