Lithology from PE-Density-Neutron Logs
When the density neutron log is recorded with a photo electric curve, it is often called a litho-density log. Most density neutron logs run today are of this type. There are a numger of lithology models availanle using combinations of these three curves.

The photo electric effect (PE) log curve is sometimes used directly for determining lithology, because it has very definitive matrix values, and linear interpolation between two end points works quite well. However there is a small porosity effect, so a quantity called the photoelectric absorption coefficient (U) is used instead:
       1: U = PE * DENS

The response equation for the absorption coefficient (U) is:
      2: U = UMA * (1 - PHIe - Vsh)
             + UW * PHIe * Sxo
             + UH * PHIe * (1 - Sxo)
             + USH * Vsh

A common assumption is that UH and UW are very small, and that the shale term can be lumped into the matrix term. Equation 7 below is more accurate in shaly zones.:

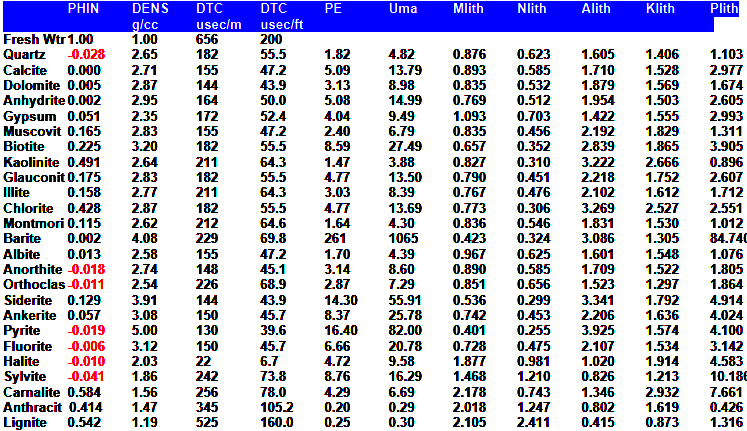
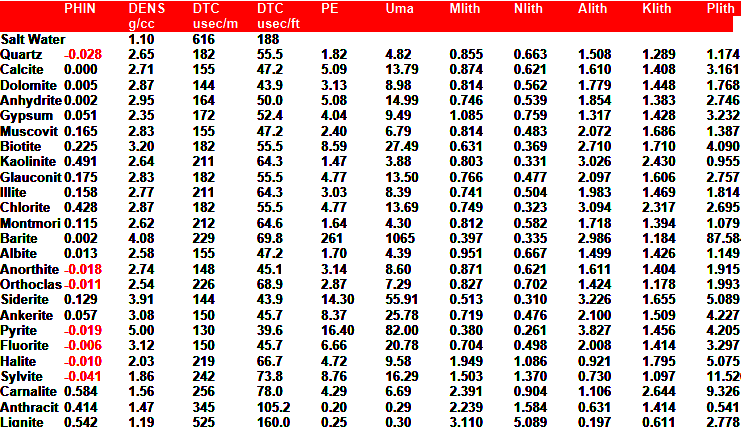
Where:
  PHIe = effective porosity (fractional)
  U = photoelectric absorption cross section (barns/cm3)
  UH = photoelectric absorption of hydrocarbon (barns/cm3)
  UMA = photoelectric absorption of matrix rock (barns/cm3)
  USH = photoelectric absorption of shale (barns/cm3)
  UW = photoelectric absorption of water (barns/cm3)
  Vsh = volume of shale (fractional)
Note - 1.0 barn = 1*10^- 24 square centimeters - pretty small cows!

COMMENTS
The Uma values can be used in crossplots with matrix density (DENSma), to determine lithology fractions in a two or three mineral model.

 
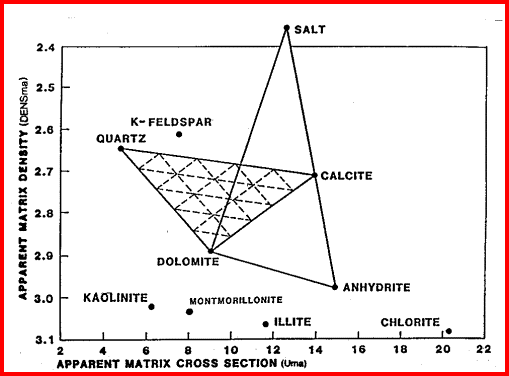
 Matrix Density vs Matrix Cross Section Crossplot for Lithology

Rock Volume from PE Density Neutron Models
 A few preliminary calcs are meeded:
      3: DENS = PHID * KD1 + (1 - PHID) * KD2
      4: DENSSH = PHIDSH * KD1 + (1 - PHIDSH) * KD2
       5: DENSma = (DENS - PHIe * DENSW - Vsh * DENSSH) / (1 - PHIe - Vsh)
       6: USH = PESH * DENSSH
      7: Uma = (PE * DENS - Vsh * USH) / (1 - PHIe - Vsh)

PE 2- Mineral Model
Linearly interpolate between any two mineral  end points and solve for Vmin1 and Vmin2. This is the ONLY mineral  model for gas zones as PE is unaffected by gas. Also excellent for oil and water zones.
      8: Vmin1 = (PE - PE2 - Vsh * PESH) / (PE1 - PE2)
      9: Vmin2 = 1.00 - Vmin1

` Uma 2- Mineral Model
Linearly interpolate between any two mineral  end points and solve for Vmin1 and Vmin2. DO NOT usel for gas zones.
      10: Vmin1 = (Uma - UMA2 - Vsh * USH) / (UMA1 - UMA2)
      11: Vmin2 = 1.00 - Vmin1

 ` DENSma 2- Mineral Model
Linearly interpolate between any two mineral  end points and solve for Vmin1 and Vmin2. DO NOT usel for gas zones.
      12: Vmin1 = (DENSma - DENS2) / (DENS1 - DENS2)
      13: Vmin2 = 1 - Vmin1

DENSma - Uma 3 - Mineral Model
Crossplot solution to three mineral end points DO NOT usel for gas zones.
See Density Log Models  for DENSma calculation, needed for this model.
      14: D = (Uma * (DENS2 - DENS1) + DENSma * (UMA1 - UMA2)
             + UMA2 * DENS1 - UMA1 * DENS2) / (UMA1 * (DENS3 - DENS2)
             + UMA2 * (DENS1 - DENS3) + UMA3 * (DENS2-DENS1))
      15: E = (D * (DENS3 - DENS1) - DENSma + DENS1) / (DENS1 - DENS2)
      16: Vmin1 = MAX(0, 1 - D - E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      17: Vmin2 = MAX(0, E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      18:Vmin3 = (1 - Vmin1 - Vmin2)

Where:
  PHIe = effective porosity from any method (fractional)
  PE = measured PE log value of rock mixture
  PE1 = PE of first mineral (fractional)
  PE2 = PE of second mineral (fractional)
  Vmn1 = relative volume of first mineral (fractional)
  Vmin2 = relative volume of second mineral (fractional)
  Vmin3 = relative volume of third mineral (fractional)
  Vsh = volume of shale (fractional)
  Uma = computed UMA value of rock mixture
  UMA1 = UMA of first mineral (fractional)
  UMA2 = UMA of second mineral (fractional)
  UMA3 = UMA of third mineral (fractional)
  DENSma = computed matrix density value of rock mixture
  DENS1 = matrix density of first mineral (fractional)
  DENS2 = matrix density of second mineral (fractional)
  DENS3 = matrix density of third mineral (fractional)
 

COMMENTS:
The relative Vmin values must be multiplied by Vrock to get absolute values of V1, V2, V3. Vrock = 1- PHIe -Vsh..

NUMERICAL EXAMPLE:
1. Assume data as follows:
PE = 1.68 barns/cm3
DENS = 2.20 gm/cc
PHIN = 0.27
U = 1.68 * 2.20 = 3.69
Uma = 1.68 * 2.20 / (1 - 0.27) = 5.20

Both PE and Uma are close to the  quartz values. If it is dolomitic sandstone, assume:
Vsh = 0.10
PHIe = 0.24
Uqrtz = 4.79
Udolo = 9.00

Vmin1 = (5.20 - 9.00) / (4.79 - 9.00) = 0.90
Vmin2 = 1.00 - 0.90 = 0.10Vrock = 1 - 0.10 - 0.24 = 0.66.

Values to plot in lithology track:
V1 = 0.90 * 0.66 = 0.60
V2 = 0.10 * 0.66 = 0.06

The rock matrix is 90% quartz, 10% dolomite, but 34% of this is made up of porosity and shale, so the actual volumes of matrix rock are reduced by this amount.

 

MATRIX ROCK PARAMETERS

 

 
Page Views ---- Since 01 Jan 2015
Copyright 2023 by Accessible Petrophysics Ltd.
 CPH Logo, "CPH", "CPH Gold Member", "CPH Platinum Member", "Crain's Rules", "Meta/Log", "Computer-Ready-Math", "Petro/Fusion Scripts" are Trademarks of the Author