|
 Permeability from STONELEY WAVE
Permeability from STONELEY WAVE
This method is reproduced from a Schlumberger petrophysical
analysis report, edited fpr clarity and consistency with
"computer-ready" math concepts. The method relies on the
presence of a Stoneley wave travel time curve from a dipole
shear or array sonic (full waveform) acoustic log.
Stoneley waves are dispersive (velocity varies
with frequency), and are generated from the interaction between
borehole and formation. At low frequency, it is called a tube-wave.
A Stoneley waveform has a frequency content of 0.1 to 3 KHz, with
most of the energy in the late arrivals at about 500 Hz.
Stoneley waves are usually detected between 0 to
20 ms on the sonic waveform. In contrast, the shear waveforms are usually
detected between 0 to 5 ms and are concentrated around 4 KHz.
The Stoneley slowness
increases due to fluid movement in porous media and mud cake around
the borehole. The mud cake effect on slowness is usually a constant
shift if the mud cake thickness is constant and if the mud is of one
type.
One of the major factors
affecting Stoneley slowness is grain modulus. If the lithology is
changing from pure calcite to dolomite or to more siliciclastic, the
effect on slowness will vary. In addition, Stoneley wave is affected
by pore fluid modulus. For instance, if fluid is changing from
liquid to gas, the predicted permeability increases by two decades.
Stoneley wave is affected by porous media fluid and by shear modulus
at low frequency. Stoneley wave slowness can be modeled in
non-permeable zones as follows:
1: DTST^2 = (DENSfluidf * DTS^2 / DENS) +
DTCfluid^2
Where:
DTST = stoneley slowness (μs/ft)
DTS = shear slowness (μs/ft)
DENS = bulk density (g/cc)
calculated from probabilistic analysis
by summing the density contriburion from all minerals and fluids
DENSfluid = mud filtrate sensity (g/cc)
DTCfluid = mud filtrate slowness (μs/ft)
By cross-plotting DTST^2
versus DTS^2 / DENS across a zero
permeability zone, the slope of the straight line is DENSfluid and
Y-intercept is DTCfluid^2. There is one condition on the linear fit:
all data on thecross plot should be above or on the fitted line.
The Stoneley permeability
index is estimated by taking the ratio of actual measured Stoneley
slowness and modeled slowness as per above model. The formula can be
written as follows:
2: STI = DTST / (((DENSfluid * DTS^2 / DENS) +
DTCfluid^2)^0.5)
Where:
STI = Permeability index from Stoneley wave travel time (fractional
- range = 0 to 1)
 Flow Zone Index (FZI)
Flow Zone Index (FZI)
This STI model is still
affected by variations in mud cake and formation fluid type.
In addition, it does not provide a means to estimate mobility or
permeability magnitude directly.
Stoneley permeability index is
not a permeability estimation, but it is an index of fluid movement
in porous media around the borehole. Since fluid movement is a
function of pore throat distribution, pore shape, and pore size, the
Stoneley permeability index is a tortuosity index only. These
factors can be combined in a concept called Flow Zone Index (FZI).
The Stoneley permeability
index Kist is a direct measurement of FZI. Since FZI approaches to
zero when Stoneley permeability index approaches to 1 in
non-permeable zones, and both of them approach to infinity when
permeability approaches to infinity, then a simple relationship can
be derived between FZI and STI as following:
3: FZI = IMF * (STI – 1)
Where:
FZI = flow zone index
IMF = flow zone index matching factor
With this equation, the only
empirical factor to match actual permeability profile is IMF. Since
the grain modulus has an effect on Stoneley slowness, IMF can be
computed in the probabilistic model by summing the volume
weighted IMF for eaach individual mineral in the model. Note: the
Schlumberger report does not indicate how the individual IMF
parameters were derived. Values quoted were:
Zone "A" Calcite = 12, Illite = 0.001, Kaolinite = 0.001, Quartz = 1.0,
Siderite = 0.0
Zone "B" Calcite = 10, Illite = 0.001, Kaolinite = 0.001, Quartz = 130,
Siderite = 0.0
Stoneley permeability can be
computed by using effective porosity and FZI with the following:
equations:
4: PERMst = MPERM * FZI^2 * (PHIe^3 / (1- PHIe)^2)
Where:
PERMst = permeability from Stonely method (md)
PHIe = effective porosity
FZI = flow zone index
MPERM = permeability calibration factor (default = 1014)
This method is valid for the
following conditions:
• Single-phase fluid in
porous media.
• Negligible temperature variation.
• Single type mud cake with fairly constant mud cake thickness.
• Sufficient logs for volumetric lithology modeling.
• Available core, MDT permeabilities or down-hole production
profile with constant draw down.
• In bad holes or severely rough surface condition, this method
is not valid any more.
This method is limited to the
DSI vertical resolution of 3.5 ft. The volume measured by the DSI is
0.5 to 1 ft thick with 3.5 ft long cylinder.
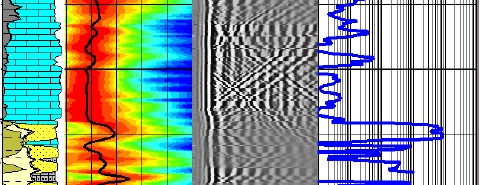
Example of permeability calculated from Stoneley wave travel
time. Lithology (Track 1), Stoneley travel time (Track 2), VDL
display (chevron patterns = fractures), calculated permeability -
nilliDarcies (Track 5).
|

