Seismic Velocity and Dipping Beds
Another typical problem in common depth point shooting is shown in the diagram below. Ray paths are shown only from reflector 3 for clarity. Normal incident points are those points on reflecting horizons which would be recorded from a common ground point, that is from a source and a receiver in the same position.

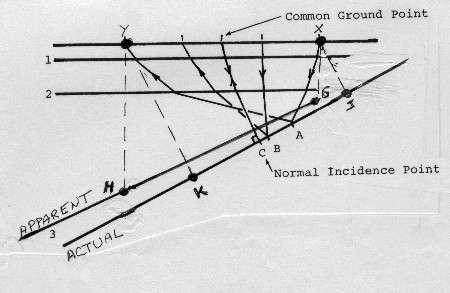
Stacking common depth point problem with dipping beds                                                                    

When we do a velocity analysis on a computer, we compare the arrival times of the incident points from the reflector. For example, from reflector 3, we measure the change in NMO from the reflection which originates at C with that which originates at B and at A. The computer derived velocity is the velocity which will take the three reflecting points, C, B, and A, and stack the reflections from them in phase.

Points A, B, and C are not common depth points, but that doesn't matter for stacking purposes. The computer derived velocity analysis forces the time of the stacked trace to be that of the zero offset or normal incident point C. The presence of dip, as on reflection 3, will obviously reduce the observed NMO between C and A. Therefore we can conclude in this example that as dip increases, we will have less NMO and the apparent velocity will be higher.

It is clear, when using seismic velocity analyses in the absence of migration, that the computed interval velocities may differ very greatly from the true interval velocities. It is just as important to use these velocities for stacking, because a true velocity or an average velocity derived from interval velocities will not move the reflections from points A, B, and C to a common point. Only an apparent, or stacking, or computer derived velocity will do the proper stacking job when beds dip appreciably.

For structural or stratigraphic interpretation, the computer derived seismic velocity functions must be reworked to compensate for dip and the effect of ray path geometry before being used. The correction procedure is called seismic migration. In the drawing below, Reflector 3 appears to be at a position given by line G-H because the vertical times Y-H and X-G are equal to the normal incidence times Y-K and X-J respectively. The steeper the dip, the worse the discrepancy becomes. Since we see line G-H on the seismic section, we underestimate dip and depth to the actual reflecting horizon.

To correct this, we note that:
      1: Sin (DIPact) = Tan (DIPapp)

Where:
  DIPact = dip of actual reflector (line G-H, degrees)
  DIPapp = dip of apparent reflector (line J-K, degrees)

By using the power of the computer, we can identify coherent reflectors, compute their apparent dips, find their true dips, and migrate all reflections from their apparent to their true positions. This is not a trivial task. When dip direction is not the same as the line of the seismic section, migration must also involve dip rotation into the line of section, referred to as 3-D migration. If seismic interval velocity does not match the sonic log, formation dip may be the reason.