|
 SOUND VELOCITY BASICS
SOUND VELOCITY BASICS
Sonic
logs are widely used for both geophysical and petrophysical
applications. The velocity of sound in rocks is considerably more
complicated than some other physical properties, such as density,
and the math presented below reflects this.
Elasticity is a property of matter,
which causes it to resist deformation in volume or shape.
Hooke's Law, describing the behavior of elastic materials,
states that within elastic limits, the resulting strain is
proportional to the applied stress. Stress is the external
force (pressure) applied per unit area, and strain is the fractional
distortion which results because of the acting force. The modulus
of elasticity is the ratio of stress to strain.
Three types of deformation can result,
depending upon the mode of the acting force. The three elastic moduli are:
Young's Modulus,
1: Y = (F/A) / (dL/L)
Bulk Modulus,
2: Kc = (F/A) / (dV/V)
Shear Modulus,
3: N = (F/A) / tanX
Where F/A is the force per unit area
and dL/L, dV/V, and tanX are the fractional strains of length,
volume, and shape, respectively.
Another
important elastic constant, called Poisson's Ratio, is defined
as the ratio of strain in a perpendicular direction to the
strain in the direction of extensional force,
4: PR = (dX/X) / (dY/Y)
Where X and Y are the original dimensions, and dX and
dY are the changes in x and y directions respectively, as the
deforming stress acts in y direction.
Velocity of
sound in a material depends on these elastic parameters.
Sound can be
propagated in rocks with several possible modes. On the surface of
the earth, various wave modes are generated by earthquakes and can
cause severe damage. In a borehole, a logging instrument emits a
sharp sound pulse, which transmits through the rock, again with
several modes of transmission. The most useful are the
compressional, shear, and Stoneley waves, the first two being
transmitted as both body waves inside the rock and surface waves
along the wellbore face.
The
measurements made by a sonic log are recorded in units of travel
time, although a velocity scale may be superimposed on some older
logs.
Geophysicists use velocity values derived from seismic or well log
data to assist in their analysis of depth, lithology, porosity, and
hydrocarbon indications. Petrophysicists use the inverse of velocity
for porosity, lithology, and hydrocarbon analysis.
Velocity is derived from travel time by the equations:
5: Vp = 10^6 / DTC
6: Vs = 10^6 / DTS
The inverse is also true:
7: DTC = 10^6 / Vp
8: DTS = 10^6 / Vs
Where:
DTC = compressional wave travel time (usec/ft or usec/m)
DTS = shear wave travel time (usec/ft or usec/m)
Vp = compressional wave velocity (ft/sec or m/sec)
Vs = shear wave velocity (ft/sec or m/sec)
The conversion factor of 10^6 accounts
for the conventional units of measurement on the sonic log –
microseconds per meter (or foot).
 BIOT-GASSMANN VELOCITY RELATIONSHIPS
BIOT-GASSMANN VELOCITY RELATIONSHIPS
The velocity of sound in a rock is related to the elastic properties
of the rock/fluid mixture and its density, according to the
Wood, Biot, and Gassmann equations.
The composite compressional
bulk modulus of fluid in the pores (inverse of fluid
compressibility) is:
9: Kf =
1/Cf = Sw / Cwtr + (1 - Sw) / Coil
_OR 9a: Kf = 1/Cf = Sw / Cwtr + (1
- Sw) / Cgas
|
RECOMMENDED PARAMETERS:
|
|
Water |
Salinity |
Cf psi-1 |
Kf psi |
Cf GPa-1 |
Kf GPa |
|
|
5000 |
0.0000040 |
250000 |
0.580 |
1.723 |
|
|
35000 |
0.0000039 |
270270 |
0.537 |
1.862 |
|
|
200000 |
0.0000027 |
344828 |
0.420 |
2.376 |
|
|
|
|
|
|
|
|
Oil |
Depth |
|
|
|
|
|
|
2000 ft 610 m |
0.0000085 |
117647 |
1.233 |
0.811 |
|
|
4000 ft 1220 m |
0.0000095 |
105263 |
1.378 |
0.725 |
|
|
8000 ft 2440 m |
0.0000116 |
86207 |
1.683 |
0.594 |
|
|
12000 ft 3660 m |
0.0000135 |
74074 |
1.959 |
0.510 |
|
|
|
|
|
|
|
|
Gas |
Depth |
|
|
|
|
|
|
2000 ft 610 m |
0.001250 |
800 |
181.422 |
0.006 |
|
|
4000 ft 1220 m |
0.000510 |
1961 |
74.020 |
0.014 |
|
|
8000 ft 2440 m |
0.000180 |
5556 |
26.124 |
0.038 |
|
|
12000 ft 3660 m |
0.000100 |
10000 |
14.513 |
0.069 |
The pore space bulk
modulus (Kp) is derived from the porosity, fluid, and matrix
rock properties:
10: ALPHA = 1 - Kb / Km
11: Kp = ALPHA^2 / ((ALPHA - PHIt) / PHIt / Kf )
The
composite rock/fluid compressional bulk modulus is:
12: Kc = Kp + Kb + 4/3 * N
Compressional and shear
velocity (or travel time) depend on density and on the elastic
properties, so we need a density value that reflects the actual
composition of the rock fluid mixture:
13: DENS = (1 - Vsh) *
(PHIe * Sw * DENSw + PHIe * (1 - Sw) * DENSh + (1 - PHIe) * DENSma)
Note that a density log reading may not be an appropriate value in
the following equations due to the effects of drilling fluid
invasion on the hydeocarbon saturation.
+ Vsh * DENSsh
Compressional velocity (Vp) and shear
velocity (Vs) are defined as:
14: Vp = KS4 * (Kc / DENS) ^ 0.5
15: Vs = KS4 * (N / DENS) ^ 0.5
16: Vst = KS4 * (DENSW * (1/N + 1/Kf)) ^ 0.5
Although it is not always a precise solution, we often invert equations
5 and 6 to solve for Kb and N from sonic log compressional and
shear travel time values.
Where:
ALPHA = Biot's elastic parameter (fractional)
Cgas = gas compressibility (1/GPa)
Coil = oil compressibility (1/GPa)
Cwtr = water compressibility (1/GPa)
DENS = rock density (g/cc)
DENSW = density of fluid in the pores (g/cc)
DTC = compressional sonic travel time (usec/m)
DTS = shear sonic travel time (usec/m)
Kb = compressional bulk modulus of empty rock frame (GPa)
Kc = compressional bulk modulus of porous rock (GPa)
Kf = compressional bulk modulus of fluid in the pores (GPa)
Km = compressional bulk modulus of rock grains (GPa)
Kp = compressional bulk modulus of pore space (GPa)
N = shear modulus of empty rock frame (GPa)
PHIt = total porosity of the rock (fractional)
Sw = water saturation (fractional)
Vp = compressional wave velocity (m/sec)
Vs = shear wave velocity (m/sec)
Vp = Stoneley wave velocity (m/sec)
KS4 = 1000 for semi-Metric units shown above - convert kg/m3 to
g/cc
The Biot-Gassmann approach looks deceptively simple. However, the major
drawback to this approach is the difficulty in determining the
bulk moduli, particularly those of the empty rock frame (Kb and
N), which cannot be derived from log data. Murphy (1991)
provided equations for sandstone rocks (PHIe < 0.35) that
predict Kb and N from porosity:
17: Kb = 38.18 * (1 - 3.39 * PHIe + 1.95 *
PHIe^2)
18: N = 42.65 * (1 - 3.48 * PHIe
+ 2.19 * PHIe^2)
These
can help overcome the lack of empty rock-frame data.
NOTE: Abbreviations used in the literature for elastic
constants vary dramatically and no consistent set was found.
The abbreviations used in this Handbook reflect those used in recent
Schlumberger papers.
CAUTION: This book uses the abbreviation "V" for
Velocity AS WELL AS for Volume, as in Vsh for volume of shale
(not velocity of shale or shear velocity). Likewise the abbreviation
K is used for permeability (eg Kmax, Kv, Kh, etc) as well as
for compressional bulk modulus. Watch the context!
IMPORTANT NOTE: The mechanical properties theory is
based on the assumption that rocks behave elastically and are
isotropic. Neither of these assumptions is actually true in
many situations. Anisotropic behaviour is common and fractured
rocks may not behave elastically
The nuts and bolts of the above equations shows three
things:
1. acoustic velocity is intimately connected to density and elastic constants
of the rock.
2. If any two of density, velocity, or an elastic constant, are known, the
others can be calculated
by rearranging the formulae.
3. Since density and the elastic constants vary with porosity, then so does
acoustic velocity for
both compressional and shear arrivals.
It is the last fact that suggests that a log of acoustic
velocity or specific acoustic travel time (sometimes called
"slowness") might be a reasonable
predictor of porosity.
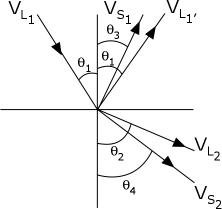
 SNELL'S LAW
SNELL'S LAW
Snell’s Law determines the path that sound energy takes when moving
from one medium to another, for example from a borehole full of mud
into a rock (as in well logging) or from one layer of rock to
another (as in seismic reflection and refraction). The law states
that:
19: sin (Incident Angle) / sin (Transmitted
Angle)
= (Incident
Velocity) / (Transmitted Velocity)
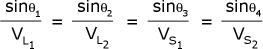
Snell's Law applies to all electromagnetic waves as
well as acoustic waves.
The critical angle is the angle of incidence that
creates refraction of sound energy along the interface between two
dissimilar media, for example along the wellbore face (as in well
logging) or along the boundary between two rock layers (as in
seismic refraction surveys). The equation is:
20: CritAngl = ArcSin (Incident
Velocity) / (Transmitted Velocity)
For the sonic log:
21: CritAngl = ArcSin (Vmud / Vrock)
= ArcSin (DTCrock / DTCmud)
Sonic logging tools consist of one or more sources of
pulsed sound energy and a number of sound detectors. The sound
travels from the source on the logging tool, through the mud in the
borehole, to the rock. Here it is refracted at the critical angle,
according to Snell’s Law, and travels in the rock parallel to the
borehole.
The source creates a compressional wave through the
mud, a portion of which undergoes mode conversion to create a shear
wave as well as the compressional wave in the rock. The shear wave
is slower than the compressional, and modern sonic log processing
can segregate and record both.
Both compressional and shear waves
refract back into the borehole, the shear converting to a
compressional wave, to be detected by the receivers in the logging
tool.
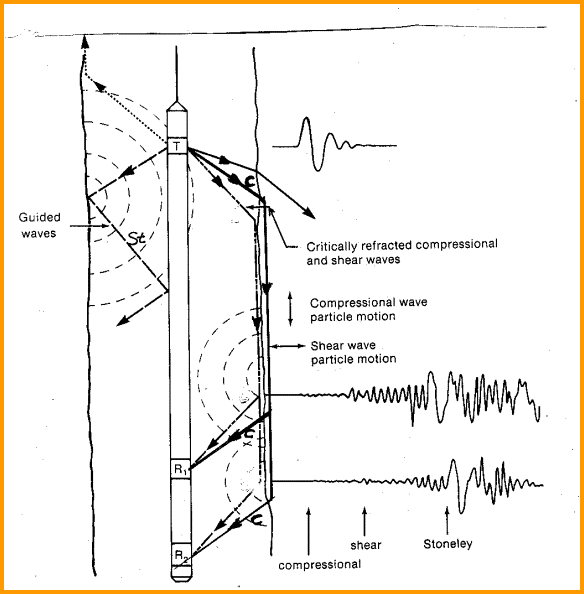
Schematic diagram of a simple sonic
log showing sound paths, following Snell's Law.
 Sound Velocity in Gases
Sound Velocity in Gases
The only sound wave passed through a gas is the compressional
wave. Its velocity is:
22: Vgas = 68.4 * (Ks * P / DENS)^0.5
Where:
DENS = density (lb/cuft)
Ks = ratio of specific heats (unitless)
P = pressure (psi)
Vgas = velocity of sound (ft/sec)
Note
that V is a Velocity here, while V is used as Volume elsewhere
in this Handbook.
 Numerical Example:
Numerical Example:
Find the velocity of sound in a gas with same composition and
under the same reservoir conditions as before, given the ratio
of specific heats equal to 1.37.
Vgas
= 68.4 * (1.37 * 1000 / 4.936) ^ 0.5 = 1140 ft / sec
DTCgas = 10 ^ 6 / 1,140 = 877 usec/ft
 Sound
Velocity in Liquids Sound
Velocity in Liquids
Again, only the compressional wave is transmitted. Velocity of
sound in water or oil can be derived from:
23: Vliq = ((144 * Gc) / (Cw * DENSliq)) ^
0.5
Where:
Cw = compressibility of liquid (psi^-1)
DENSliq = density of liquid at downhole conditions
(lb/cuft)
Gc = acceleration of gravity = 32.7 ft/sec ^ 2
Vliq = velocity of sound in liquid (ft/sec)
Cw
must usually be found from laboratory measurements.
 Numerical Example:
Numerical Example:
Find the sound velocity of oil and water from the previous example.
Voil = ((144 * 32.17) / (3.0*10^-6 * 71.70)) ^ 0.5 = 4,640 ft/sec
DTCoil = (10 ^ 6) / Voil = 206 usec/ft
Vwater
= ((144 * 32.17) / (2.0*10^-6 * 78.80 )) ^ 0.5 = 5,450 ft/sec
DTCw = (10^6) / Vwater = 184 usec/ft
 Sound
Velovity in Solids
Sound
Velovity in Solids
The velocity of longitudinal (compressional) waves in solids can
be predicted from the following two equations.
24: Vp = 68.4 * (((K + 4/3 * N) / DENS) ^ 1/2)
OR: 24A: Vp = 68.4 * (((Y * (1 - N) / (DENS * (1 - 2 * N) * (1 - N))
^ 1/2)
Where:
K = bulk modulus of elasticity (psi)
DENS = density (lb/cuft)
N = shear modulus or modulus or rigidity (psi)
Vp = compressional velocity (ft/sec)
Y = Young's modulus (psi)
The
transverse (shear) wave velocity is defined by the following two
equations:
25: Vs = 68.4 * ((N / DENS) ^ 1/2)
OR 25A: Vs = 68.4 * (((Y / DENS) / 2 * (1 + PR)) ^ 1/2)
Where:
DENS = density (lb/cuft)
N = shear modulus or modulus or rigidity (psi)
PR = Poisson's ratio (unitless)
Vs = shear wave velocity (ft/sec)
To
translate these formulae into metric, convert density into gm/cc,
velocity to Km/sec and the various moduli to megabars, and change
the constant terms to 1.0. To
convert moduli in megabars to psi, multiply by 6.89 * 10^-6. To
convert megabars to Kilopascals, multiply by 10^4. Also note
that 1 GigaPascal (GPa = 10^10 dynes/cm^2.
 Sound
Velocity in Mixtures -
WYLLIE TIME AVERAGE EQUATION Sound
Velocity in Mixtures -
WYLLIE TIME AVERAGE EQUATION
An equation similar to that for density can be generated for sound
velocity of mixtures. It is a summation of travel time weighted
by volume and not a summation of velocity components:
26: DTC = Sum (DTCi * Vi)
Where:
DTC = travel time of mixtures (usec/ft or usec/m)
DTCi = travel time of ith component (usec/ft or usec/m)
Vi = volume of ith component (fractional)
This
is called the Wyllie time average equation and is true for many
situations where the components are not very compressible, such
as oil, water, sandstone, and shale. It does not work too well with
gas under low pressure. This formula is an empirical relationship
and is not rigorous, and is therefore, not a law of physics.
The
expansion of this formula for log analysis parallels the density
formula:
27: DTC = PHIe * (1 - Sw) * DTCh
+ PHIe * Sw * DTCw
+ Vsh * DTCsh
+ (1 - PHIe - Vsh) * DTCma
|
Table 1: KS8 – DTS / DTC Multiplier |
|
Coal |
1.9 to 2.3 |
|
Shale |
1.7 to 2.1 |
|
Limestone |
1.8 to 1.9 |
|
Dolomite |
1.7 to 1.8 |
|
Sandstone |
1.6 to 1.7 |
28:
KS8 = SUM (Vxxx * (DTS?DTCmultiplier))
29: DTSsyn = KS8 * DTCsyn
Where:
DTC = compressional travel time of composite material (usec/ft or usec/m)
DTS = shear travel time of composite material (usec/ft or usec/m)
DTCh = travel time of hydrocarbon (usec/ft or usec/m)
 DTCma = travel time of matrix rock (usec/ft or usec/m)
DTCma = travel time of matrix rock (usec/ft or usec/m)
DTCsh = travel time of shale (usec/ft or usec/m)
DTCw = travel time of water (usec/ft or usec/m)
PHIe = porosity (fractional)
Sw = water saturation (fractional)
Vsh = shale volume (fractional)
Vxxx = volume of each mineral present, normalized so that
SUM(Vxxx) = 1.0
(DTS/DTCmultiplier) = Vp/Vs ratio for a particular mineral (Table 1)
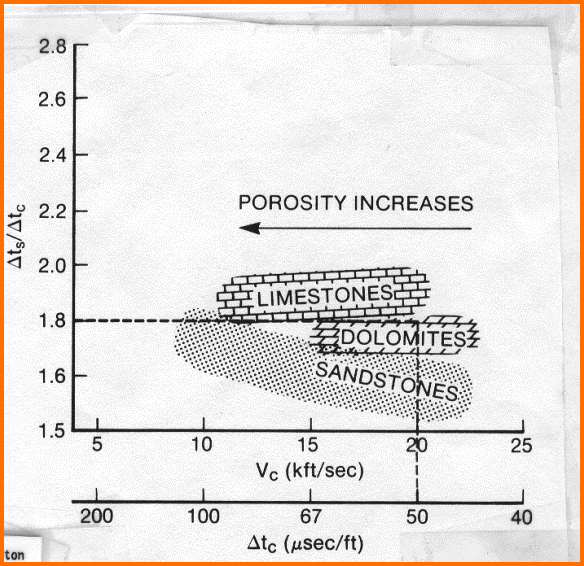
This
expansion works well as a predictive tool with oil or water in the
porosity, as the travel time of sound in liquids is quite
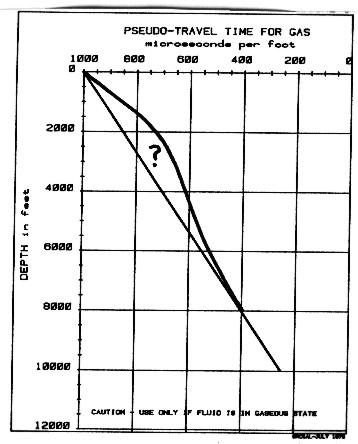
predictable. Equation 21: Vgas = ((Ks * P) ^ 1/2) / DENS,
where K is ratio of specific heats and P is pressure, looks like a
good solution for finding DTCh for gas zones. However Ks is not
usually available and some other solution is often needed. The
Biot-Gassmann equations are often preferred, empirical values for
DTCh are also used, as in the graph at the right..
 NUMERICAL EXAMPLES - Biot-Gassmann and Wyllie Equations
NUMERICAL EXAMPLES - Biot-Gassmann and Wyllie Equations
Combining equations 9 through 12, we get:
28: Kc = Kb + ((1 - Kb / Km) ^ 2) / (PHIe / Kf + (1 - PHI) / Km
- Kb / (Km ^ 2))
 Hard Rock Example - Gassmann
Hard Rock Example - Gassmann
Given:
Dolomitic limestone with 20% porosity at 10,000 feet
grain density = 2.78 gm/cc
acoustic velocity = 14,000 ft/sec at 100% water saturation = 71.4
usec/ft
bulk density = 2.44 gm/cc
formation water = 200,000 ppm total dissolved solids
reservoir temperature = 240 degrees F
reservoir pressure = 4700 psi
What
percent change in velocity could be expected if 75% of the pore
space were filled with methane gas?
0.
Convert velocity to cm/sec.
Vp = 14000 * 0.3048 * 100 = 426720 cm/sec
1.
Invert the velocity equation and solve for Kc (sometimes referred
to as the space modulus M) for 100% water-bearing condition.
Kc = (Vp ^ 2) * DENS = 426750 *
426720 * 2.44 = 44.5*10^10 dynes/cm2 = 44.5 GPa
2.
Determine Km from handbook data.
dolomite = 82 *10^10 dynes/cm2 (82 GPa)
limestone = 67 * 10^10 dynes/cm2
(67 GPa)
For
this example, Km was estimated to be 74.5 * 10^10 dynes/cm2
(74.5 GPa) because
the rock was a mixture of limestone and dolomite.
3.
Estimate Kb.
Cb = 3.7*10^-6 psi-1 from handbook data
Kb = 1 / Cb = 1.86*10^10 dynes/cm2 (1.86 GPa)
4.
Determine fluid properties at reservoir conditions.
Water compressibility (Cw) was estimated to be:
Cw = 2.26*10^-6 psi-1 from handbook data
Kw = 1 / Cw = 3.05 * 10^10 dynes/cm2 (3.05 GPa)
Water
density = 1.085 gm/cc.
Gas
density was estimated to be 0.157 gm/cc.
Gas compressibility (Cg) was computed from:
Cg = 161*10^-6 psi-1 from handbook data
Kg = 1 / Cg = 0.0428 * 10^10 dynes/cm2 (0.0428 GPa)
Gas-water
combination properties.
DENSf = 0.25 * (1.085) + 0.75 * (0.157) = 0.389 gm/cc
Kf
from the Wood equation.
1 / Kf = Sw / Kw + Sg / Kg
Kf = 0.0568*10^10 dynes/cm2 (0.0568 GPa)
5.
Solve Gassmann equation for Kb at Sw = 100%.
Kb @ 100% water saturation = 44.5 * 10^10 - ((1 - 1.86*10^10 / 74.5 * 10^10) ^ 2) /
(0.2 / 3.05 * 10^10 + 0.8 / 74.5 * 10^10 - 1.86 / (74.5 * 10^10)
^ 2
= 32.9 * 10 ^ 10 dynes/cm2 (32.9 GPa)
6.
Solve this equation for Kc with combination gas/water conditions.
Kc @ 75% gas saturation = 44.5 * 10^10 - ((1 - 1.86 * 10^10 / 74.5 * 10^10) ^ 2) /
(0.2 / 0.0568*10^10 / 74.5 * 10^10 - 1.86 / (74.5*10^10) ^ 2)
= 33.2*10^10 dynes/cm2 (33.2 GPa)
7.
Solve density equation for gas/water combination.
DENS @ 75% gas saturation = 0.2 * (0.389) + 0.8 * (2.78) = 2.30 gm/cc
8.
Solve for Vp for Sg = 0.75.
Vp @ 75% gas saturation = (33.2 * 10^10) ^ 0.5 / 2.30 = 3.80 * 10^5 cm/sec = 12,500
ft/sec
Utilizing
this methodology and the stated assumptions, there would be an
approximate 10% change in velocity (14,000 - 12,500 / 14,000)
from a 100% water saturated zone to one that has identical rock
properties but 75% gas saturation in the pore space. As a matter
of interest, if the rock frame compressibility were assumed to
be 5.0 * 10^-7 psi-1, the computed gas/water-bearing velocity
would be 13,100 ft/sec. This is only 7% slower than the observed
water-bearing velocity and helps demonstrate the sensitivity of
the calculation to the assumption of rock frame modulus.
 Soft Rock Example - Gassmann
Soft Rock Example - Gassmann
Given:
Tertiary sandstone with 32% porosity.
grain density = 2.65 gm/cc at 7,000 ft
acoustic velocity = 8,130 ft/sec = 123 usec/ft
bulk density = 2.17 gm/cc at 100% water saturation
formation water = 225,000 ppm TDS
reservoir temperature = 184 degrees F
reservoir pressure = 7,300 psi
estimated net effective stress < 1,000 psi
What
percentage change in velocity could be expected if 75% of the
pore space were filled with methane gas (gas gravity 0.8)?
Kc = 13.3 * 10^10 dynes/cm2
(13.3 GPa)
Km taken as 37.9 * 10^10 dynes/cm2 (37.9 GPa)
Estimated Cb = 3.5 * 10^-6 psi^-1 from experience.
Compressibility
values on poorly consolidated formations are difficult to obtain.
It is believed that many operators are attempting to measure and
catalogue such data. However, most of these data are being held
confidential.
Kb = 1 / Cb = 1.97 * 10^10 dynes/cm2 (1.97 GPa)
Kw = 3.71 * 10^10 dynes/cm2 (3.71 GPa)
Kg = 0.186 * 10^10 dynes/cm2 (0.186 GPa)
Kf = 0.244 * 10^10 dynes/cm2
DENSg = 0.32 gm/cc
DENSw = 1.15 gm/cc
DENSf = 0.528 gm/cc
Kb @ 100% water saturation = 4.59 * 10^10 dynes/cm2
(4.59 GPa)
Kc @ 75% gas saturation = 5.27 * 10^10 dynes/cm2
(5.27 GPa)
DENS @ 75% gas saturation = 1.97 gm/cc
Vp @ 75% gas saturation = 5,370 ft/sec
The
velocity change computed with these assumptions is approximately
34%. However, the computed velocity of 5,370 feet per second,
or 186 microseconds per foot, compares reasonably well to observed
sonic log values in gas zones having rock and reservoir properties
similar to the assumptions made in this calculation.
As
a matter of interest, if the bulk compressibility of the rock frame
is assumed to be 3.0 * 10^-5 psi-1, or an increase of nearly an
order of magnitude, the computed Gasmann velocity for 75% gas
is 5,000 feet per second. This is an additional 4.5% decrease
in velocity from the water-bearing case.
 Hard Rock Example - Wyllie
Hard Rock Example - Wyllie
Same rock properties as Case 1:
porosity (PHIe) = 0.20
shale content (Vsh) = 0.00
water saturation (Sw) = 0.25
shale travel time (DTCsh) = 70 usec/ft
matrix travel time (DTCma) = 44 usec/ft
water travel time (DTCw) = 189 usec/ft
gas pseudo-travel time (DTCh) = 250 usec/ft
Solving
the equation:
DTC = (1 - 0.20 - 0.00) * 44 + 0.00 * 70 + 0.20 * 0.25 * 189
+ 0.20 * 0.75 * 250
= 82.15 usec/ft
Vp = 10^6 / DELT = 12,170 ft/sec
(compared to 12,500 ft/sec for Gasmann equation)
 Soft Rock Example - Wyllie
Soft Rock Example - Wyllie
Same rock properties as Case 2:
porosity (PHIe) = 0.32
water saturation (Sw) = 0.25
shale volume (Vsh) = 0.10
shale travel time (DTCsh) = 90 usec/ft
matrix travel time (DTCma) = 55.5 usec/ft
water travel time (DTCw) = 189 usec/ft
gas pseudo-travel time {DTCh) = 550 usec/ft
Solving
the equation:
DTC = (1 - 0.32 - 0.10) * 55.5 + 0.10 * 90 + 0.32 * 0.25 * 189
+ 0.32 * 0.75 * 550
= 188.3 usec/ft
Vp = 10^6 / 188.3 = 5,310 ft/sec
(compared to 5,370 ft/sec for Gasmann equation)
Note
that the result depends largely on the choice of gas pseudo-travel
time, and this is subject to some error in judgment.
|

