|
 Calibrating Porosity to Core
Data
Calibrating Porosity to Core
Data
The proof of a log analysis is the degree to which the porosity
matches core analysis porosity. The easiest way to check this
is to plot the core analysis porosity on top of the log analysis
on the same depth plot. If the overlay is quite good, no more needs to be done except show off the comparison
and brag a bit. If the core is off depth to the log porosity,
shift the core depths appropriately and re-display the results.
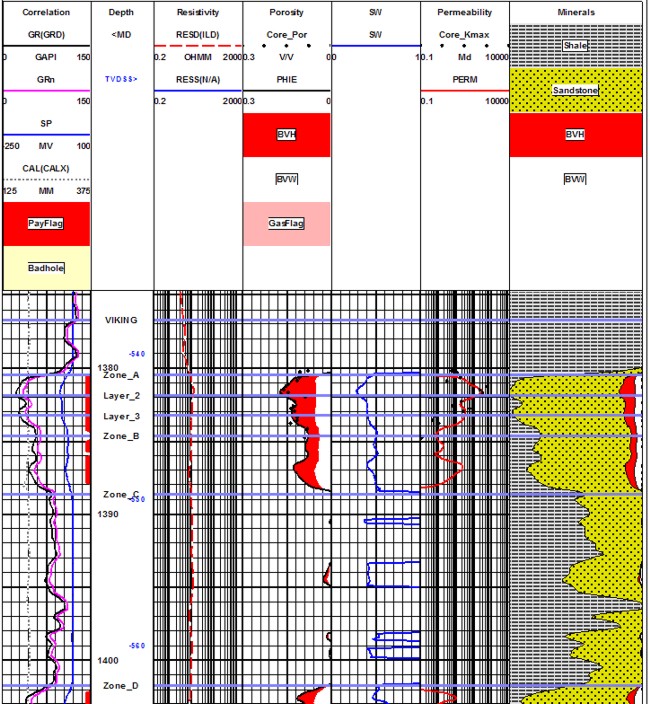
Comparison of Core Porosity with Log Analysis Porosity -
black dots are
core, smooth lines are log analysis.
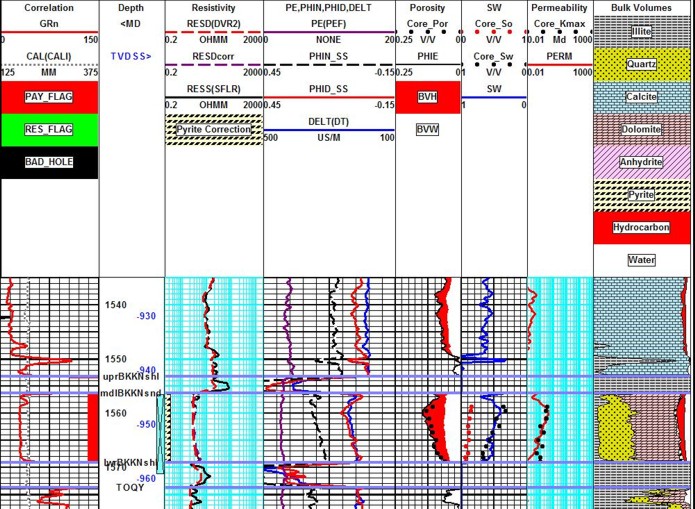
Bakken “Tight Oil” example showing core porosity (black dots), core oil saturation (red dots).
core water saturation (blue dots), and permeability (red dots). Note
excellent agreement between log analysis and core data. Separation
between red dots and blue water saturation curve indicates
significant moveable oil, even though water saturation is relatively
high. Log analysis porosity is from the complex lithology model and
lithology is from a 3-mineral PE-D-N model using quartz, dolomite
and pyrite.
If
the comparison is poor, there are three choices. First make sure
the core data is on depth with the logs and that each log curve
is on depth with each other.
 CHOICE 1
(preferred): Adjust shale, matrix, and fluid parameters
in the log analysis model until a better match is achieved. This
may take several attempts and may require choosing a different
mathematical model or mineral assemblage.
CHOICE 1
(preferred): Adjust shale, matrix, and fluid parameters
in the log analysis model until a better match is achieved. This
may take several attempts and may require choosing a different
mathematical model or mineral assemblage.
 CHOICE 2: Crossplot core porosity vs log analysis porosity, and
find a regression line that corrects the log result to the core,
of the form:
CHOICE 2: Crossplot core porosity vs log analysis porosity, and
find a regression line that corrects the log result to the core,
of the form:
1: PHIcorr = K1 * PHIe + K2
Where:
PHIcorr = corrected porosity (fractional)
PHIe = effective porosity (fractional)
K1 = slope of regression line
K2 = intercept of regression line
The regression should be the reduced major axis (RMA) method (see
and not a simple least squares regression. RMA
assumes errors occur in both axes and not just in the Y axis data.
An eyeball line may be best as stray outliers can be discarded
quickly. The before and after crossplots can be used to document
the change. Do not use the regression unless the error is reasonably
low (R-squared > 0.8 or so).
CAUTION: Core data must be depth
matched to logs before you do this. And some core data is faulty
or not spread across a wide enough range of values. Porosity or
shale laminations thinner than the tool resolution cause a fair
scatter on crossplots and depth plots. There is no direct
solution to obtain a better match except to match average
porosity from log analysis with average porosity from the core.
 CHOICE 3: Perform the regression on a single input log curve instead
of on PHIe, or separately on several curves. Pick the regression
with the least standard deviation or highest R-squared. This creates
a new log analysis model that may be used locally instead of the
universal methods described in this Chapter.
CHOICE 3: Perform the regression on a single input log curve instead
of on PHIe, or separately on several curves. Pick the regression
with the least standard deviation or highest R-squared. This creates
a new log analysis model that may be used locally instead of the
universal methods described in this Chapter.
You might need a multi-variant regression to account for all the
minerals and fluids, or even a Principal Components analysis to
obtain a statistical solution.
It
is also common to calibrate simple log analysis porosity methods to crossplot
methods, which in turn might be calibrated to core, by overlay plots or regression. The calibration
can then be carried to wells that do not have sufficient data
for crossplot analysis.
 Calibrating Porosity to PETROGRAPHIC
Data
Calibrating Porosity to PETROGRAPHIC
Data
There are many occasions when core analysis porosity is not available
for calibration of log results. The next best data set is petrographic
thin section visual porosity analysis. This usually excludes micro-porosity
so a regression of thin section porosity vs log analysis porosity
will give useful porosity (PHIuse) instead of PHIe. Most people
like this result. Thin sections can often be made from sample
chips when no core exists. Thin section samples are tiny and it
is sometimes difficult to scale-up these results to the whole
reservoir. A large number of samples in varying facies can give
statistically meaningful results. A few samples are probably useless.
|
|
15X
Magnification |
100X
Magnification |
|
Thin Section Images |
| |
Depth,
ft. |
9403.70 |
9407.00 |
9413.50 |
9419.20 |
Porosity
@ NOB (%) |
12.4 |
8.2 |
10.9 |
5.0 |
Air
Perm. @ NOB (md) |
0.296 |
0.034 |
0.338 |
0.0054 |
Grain
Density (g/cc) |
2.81 |
2.83 |
2.82 |
2.79 |
PRIMARY
MINERAL |
|
|
|
|
Dolomite |
60.0 |
81.2 |
80.0 |
79.6 |
Calcite |
Tr |
0.0 |
0.0 |
0. |
Anhydrite |
1.2 |
0.4 |
0.8 |
0.0 |
Pyrite |
2.0 |
1.6 |
1.6 |
1.6 |
Quartz |
0.0 |
0.0 |
0.0 |
0.0 |
Feldspar |
0.0 |
0.0 |
0.0 |
0.0 |
Authigenic
Clay |
0.0 |
0.0 |
0.0 |
0.0 |
Bitumen |
0.0 |
0.0 |
0.0 |
0.0 |
Other |
0.0 |
0.0 |
0.0 |
0.0 |
Total |
63.2 |
83.2 |
82.4 |
81.2 |
SILCLASTICS |
|
|
|
|
Mono
Quartz |
8.8 |
2.0 |
4.4 |
7.2 |
Poly
Quartz |
0.0 |
0.0 |
Tr |
0.0 |
Plagioclase |
2.0 |
0.8 |
0.8 |
1.6 |
Potassium
Feldspar |
3.6 |
1.2 |
0.8 |
3.2 |
Chert |
0.0 |
0.0 |
0.0 |
0.0 |
Rock
Fragments |
0.0 |
0.4 |
0.0 |
0.0 |
Shale
Fragments |
0.0
|
Tr |
0.0 |
0.0 |
Muscovite |
Tr |
0.4 |
0.0 |
Tr |
Biotite |
2.0 |
0.8 |
0.0 |
0.0 |
Heavy
Minerals |
0.0 |
Tr |
0.0 |
0.4 |
Carbonaceous
Fragments |
1.2 |
0.4 |
Tr |
Tr |
Glauconite |
0.0 |
0.0 |
0.0 |
0.0 |
Detrital
Clay Matrix |
3.2 |
1.6 |
1.6 |
1.2 |
Other |
0.0 |
0.0 |
0.0 |
0.0 |
Total |
20.8 |
7.6 |
7.6 |
13.6 |
POROSITY |
|
|
|
|
Primary
Interparticle |
0.0 |
0.0 |
0.0 |
0.0 |
Primary
Intraparticle |
0.0 |
0.0 |
0.0 |
0.0 |
Secondary
Intraparticle
(Carbonate Grains) |
0.0 |
0.0 |
1.2 |
0.0 |
Tertiary
Intraparticle
(Carbonate Grains) |
0.0 |
0.0 |
0.0 |
0.0 |
Secondary
Intraparticle
(Siliciclastic) |
Tr |
0.0 |
Tr |
0.0 |
Vugular |
0.0 |
0.0 |
Tr |
0.0 |
Intercrystalline |
16.0 |
9.2 |
8.4 |
3.6 |
Micropores |
0.0 |
0.0 |
0.0 |
0.0 |
Fracture |
0.0 |
0.0 |
0.4 |
0.8 |
Secondary
Intracrystalline |
Tr |
Tr |
0.0 |
0.4 |
Total |
16.0 |
9.2 |
10.0 |
5.2 |
|
|
|
|
|
|
100.0 |
100.0 |
100.0 |
100.0 |
Typical Thin Section Point Count Analysis with
primary, secondary, and non-useful porosity breakdown
Not all thin section reports are as detailed as this one. Scanning
electron micrograph data (SEM) is also widely used, in the same
way as thin section data.
 Calibrating Porosity to SAMPLE
DESCRIPTIONS
Calibrating Porosity to SAMPLE
DESCRIPTIONS
Porosity ranges as seen by microscopic examination of samples
are also used as a guide. This may be useful in the absence of
more quantitative data or where rough hole conditions make log
analysis ambiguous. The black bar graph in the illustration
below shows visual
porosity spanning three ranges. Log analysis should at least see
porosity in the same zones and somewhat in proportion to the variations
in visual porosity values.
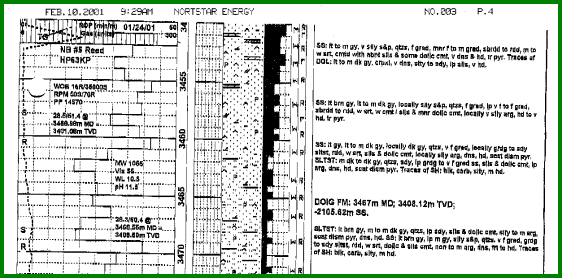
Sample Description Log with Microscopic Visual Porosity
(black bar graph in center of plot)
|

