|
 CALIBRATING Water
Saturation
CALIBRATING Water
Saturation
Log analysis water
saturation can be calibrated by comparing calculated results to capillary pressure data from special
core analysis. It has been a tradition to use the minimum water saturation from the cap
pressure curve as a guide to irreducible water saturation,
and to use this value (at a given porosity) to calibrate the
log analysis.
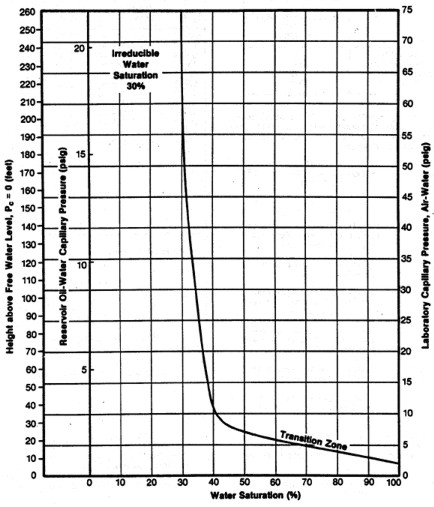
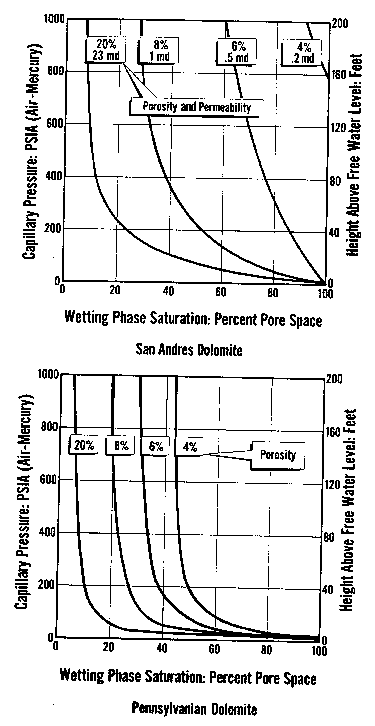  Capillary pressure curves
for various rock types, showing both
Capillary pressure curves
for various rock types, showing both
pressure and height above
free water on the vertical axes
This technique ONLY applies in relatively high quality
reservoirs and at some distance above the oil-water contact.
In
poorer quality reservoirs, saturation varies considerably higher
than the minimum as we approach the oil-water contact. The more
rigorous method is to convert the capillary pressure versus water
saturation graph to a height above free water versus saturation
graph, and use the depth dependant data set to calibrate log derived
water saturation.
The water saturation for a given core plug is taken from the
graph (or associated data listing) at the height above free water
that is appropriate for the well in question. Notice that each
cap pressure curve has an associated porosity and permeability
value. Low permeability and low porosity rocks have high natural water
saturation.
In
fact, it is possible for a rock to be 100% wet in the middle of
an oil zone merely because the porosity is too low for oil to
get into the pores. No water will be produced from these intervals
because the irreducible water saturation is also 100%. The cap
pressure curve at top right represents such a rock - it would
have to be 180 feet above free water before it could take on even
1% oil saturation. Any similar rock closer to the water zone would
be 100% wet, but adjacent layers in the same reservoir could have
better rock properties (higher porosity)
and therefore lower water saturation.
The
best way to see the relationship is to crossplot porosity vs cap
pressure water saturation at some arbitrary height above free
water. If a reservoir is very thick, make several crossplots at
different heights. Make similar plots for the computed log analysis
results and compare them to the cap pressure crossplots. Data
sets must be segregated by rock type or pore geometry to be meaningful.
A
typical plot for a sandstone in which porosity varies with shaliness
is shown below. Notice that the data follows a good hyperbolic
trend in the higher porosity and trails downward to a lower hyperbola
as porosity decreases, indicating a different rock type or pore
geometry. The data at extreme right with high porosity is from
the water zone.
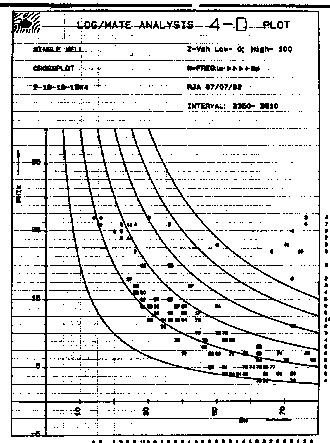 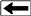 Porosity vs saturation crossplot Porosity vs saturation crossplot
An
overlay of cap pressure derived data (not shown) would confirm
or refute the log results.
First,
be sure the two data sets are from similar rock types and that
only one rock type is represented on each graph. If the trend
lines defined by the hyperbolas are different, you must revise
the log analysis (or discount the cap pressure data as "not
representative").
This
may involve changing any or all of the following: Vsh, PHIe, RW,
A, M, N, temperature, gas correction logic, or the saturation
model. Clearly there is no unique solution and an "eyeball"
best fit is all you can expect.
Some
analysts have tried to create depth plots of cap press water saturation
based on porosity and height above free water to compare with
log analysis results. This is a very difficult and seldom proves
very much. The crossplot approach is a more statistical view and
easier to defend.
 SATURATION - HEIGHT CURVES
SATURATION - HEIGHT CURVES
To convert from laboratory
air-brine measurements to reservoir conditions, we need to use the
following relationship:
1: Pc_res = Pc_lab * (SIGow * cos (THETAow)) / (SIGgw
* cos (THETAgw)
 Typical
values for air-brine conversion to oil-water are: Typical
values for air-brine conversion to oil-water are:
SIGow = 24 dynes/cm
THETAow = 30 deg
SIGgw = 72 dynes/cm
THETAgw = 0 deg
Giving: Pc_res = 0.289 * Pc_lab
Using reservoir (oil-water) Pc
values:
2: H = KP15 * Pc_res / ΔDENS
Where:
Pc_res = capillary pressure at
reservoir (psi or KPa)
H = capillary rise (ft or meters)
ΔDENS = density difference (gm/cc)
KP15 = 2.308 (English units)
KP15 = 0.1064 (Metric units)
|
Sw %
|
Pc_lab |
Pc_res |
H |
|
100 |
2 |
0.578 |
6.9 |
|
90 |
3 |
0.867 |
10.4 |
|
80 |
4 |
1.16 |
13.9 |
|
70 |
5 |
1.45 |
17.4 |
|
60 |
6 |
1.73 |
20.8 |
|
50 |
7 |
2.02 |
24.2 |
|
45 |
8 |
2.31 |
27.7 |
|
40 |
10 |
2.89 |
35 |
|
35 |
27 |
7.8 |
94 |
|
30 |
75 |
21.7 |
260 |
 Example of conversion of lab air-brine capillary
pressure data to reservoir conditions, then into saturation-height
H; results plotted in graph above.. Example of conversion of lab air-brine capillary
pressure data to reservoir conditions, then into saturation-height
H; results plotted in graph above..
All of the above assumes the lab data is an air-brine
measurement. For mercury injection capillary, pressure (MICP) measurements,
the density of the non-wetting phase (mercury) is 13.5 g/cc, so ΔDENS
is much larger than the air-water case. As a result, Pc values from
an MICP measurement are about 13.5 times higher than an air brine
measurement (for the same SW value in the same core plug). To
compare an air-brine cap pressure curve to an MICP curve, it is
merely necessary to change the Pc scale on one of the graphs by the
appropriate factor, or to convert both Pc scales to a
saturation-height scale.
When H is calculated at a number of points on the Pc curve, the
resulting graph of H vs SW is known as a saturation-height curve and
can be plotted on a depth plot of log data or results by setting H =
0 at the base of transition zone on the logs. This assumes a uniform
porosity-permeability regime, which is seldom encountered in real
life, so more complicated methods are needed to superimpose the saturation
values from multiple Pc curves.
If cap pressure curves are available at various depths in the
reservoir, the pressure axis of each curve is converted to height
above free water. Then the saturation from each curve is selected
from the graph with respect to the sample's position above the water
contact. These saturations are then plotted with respect to the
sample depths onto the log analysis depth plot, as shown in the
example below.
The example below was prepared by Dorian Holgate during one of our
joint projects.
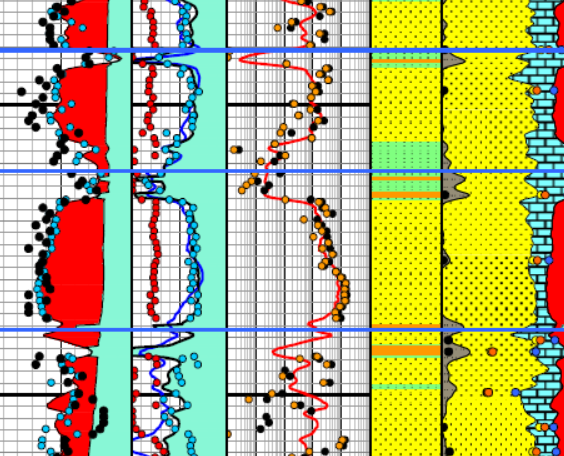
Enlarged image of log analysis depth plot showing porosity,
saturation, permeability, and lithology tracks over a conventional
oil-bearing sandstone. Black dots are conventional core porosity and
permeability. Orange dots show porosity of samples used for cap
pressure measurements and the water saturation for those samples,
chosen from their respective height above free water curve.
The orange dots match the log analysis water saturation (blue curve)
very closely everywhere.
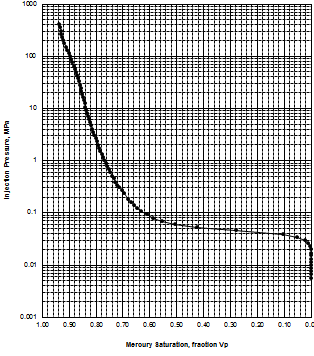
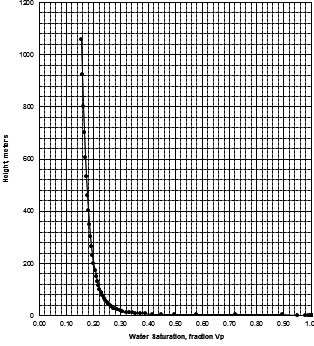
MICP capillary pressure curve (left) and equivalent height above
free water version (right) for the sample just above the oil water
contact on the above example. The reservoir is only 30 meters thick,
so we are only interested in a very small portion of these graphs,
near the bottom of each. The graph has no resolution at low height
values so it is easier to use the equivalent table of values, or
replot the data on a more appropriate scale.
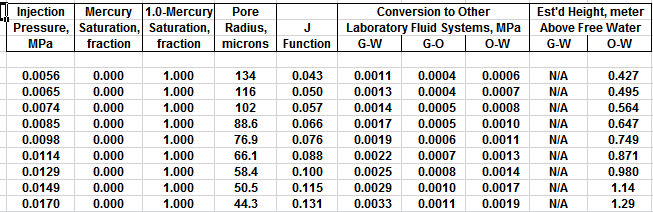
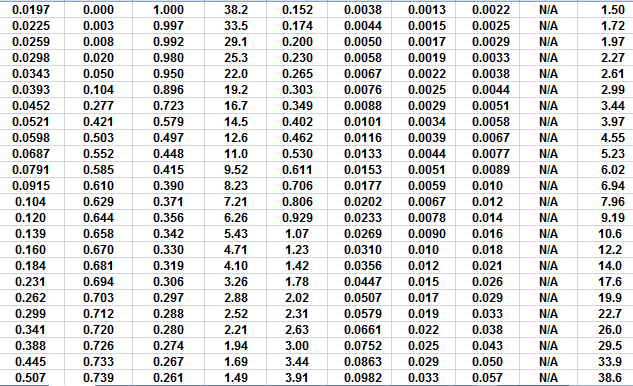
The first Pc sample above the oil-water contact is at a height of
4.5 meters above the contact. The nearest height in the table is
4.55 meters (column 10) and the corresponding saturation (column 3)
is 0.497. Use interpolation or plot a detailed graph for better
accuracy. Repeat this for each sample and its respective data table.
It has been traditional to look at the minimum water saturation on a
cap pressure curve and to call it irreducible water saturation (SWir).
In the above example, we don't see the minimum until 600 to 800
meters above the oil -water contact, and this reservoir is only 30
meters thick. The true irreducible water saturation is much higher
than the minimum on the graph because we are so close to the
contact.
The true irreducible saturation is defined by the height versus SW
curve for each sample, and not by the minimum SW. If porosity,
permeability, pore geometry, grain size, sorting vary in a
reservoir, you need a height versus SW curve for each rock type, and
a reliable method for identifying those rock types by using a log
analysis algorithm or curve shape pattern.
|

