Amplitude Versus Offset (AVO)
A technique used to differentiate seismic reflection events caused by lithology changes from those caused by fluid changes is called amplitude versus offset, or AVO, processing. The effect is caused by the fact that the reflected energy depends not only on the acoustic impedance but also on the angle of incidence of the reflecting energy.

The contribution of this second effect is often ascribed to the difference between Poisson's ratio of the layers. However, the equations clearly show the cause to be the difference in compressional velocities:

For vertical or non-vertical incidence:
_____1: K = (Vavg - Vo) / DEPTH
_____2: ANGLE = Arctan ((DEPTH * X + Vo * X/K)/(DEPTH^2 + 2*Vo*DEPTH / K - X^2 / 4))
_____3: Vrat = Vc2 / Vc1
__OR 3a: Vrat = DTC1 / DTC2
_____4: Drat = DENS2 / DENS1
_____5: C = (Vrat^2 + (1 - Vrat^2) / (Cos(ANGLE))^2) ^ 0.5
_____6: Refl = (1 - Vrat * Drat * C) / (1 + Vrat * Drat * C)

C = 1 for vertical incidence.

Poisson's ratio has the same contrast as compressional velocity when a liquid is replaced by a gas saturation. This is true because Poisson's ratio is a function of compressional to shear velocity ratio, and shear velocity doesn't change much with changes in fluid content.

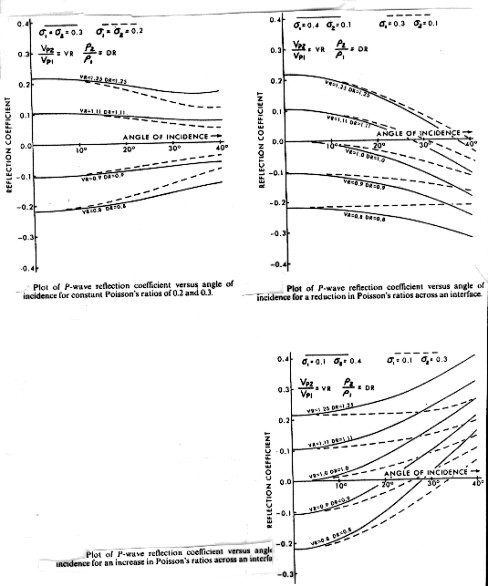
The net result is the same, no matter how it is described. For constant Poisson's ratio above and below a boundary, amplitude decreases with offset. If the upper layer has a higher Poisson's ratio than the lower, positive peaks decrease in amplitude and could go negative, while negative peaks get larger. The reverse takes place when Poisson's ratio contrast is reversed.

Amplitude versus offset schematic

There are other causes of amplitude versus offset variations:
   1. source directivity and array effects
   2. receiver arrays
   3. near surface velocity variations
   4. geometrical spreading
   5. propagation loss of high frequencies (earth filtering)
   6. dispersive phase distortion
   7. velocity anisotropy
   8. waveform interference (thin beds)
   9. short period multiple interference
   10. reflector curvature
   11. processing effects (moveout stretch, time variant scaling, etc.)

Some adequate accounting or control must be given for each of these effects in order to relate the remaining amplitude variation to reflectivity changes. Model studies are an essential element in deciding if these other effects have been properly corrected. Synthetic seismograms made this way will show the effects of amplitude versus offset. The conventional synthetic seismogram might tie the near trace data, but should not be expected to always agree well with the stacked data or the far trace data.