|
 IMMATURE OIL Shale BAsics
IMMATURE OIL Shale BAsics
The immature oil shale case is shown on the rest of this
web page. See
tight oil plays for the mature
kerogen special case.,
The
distinguishing characteristic of an immature "oil shale" is that it
contains significant organic carbon but no free oil or gas. This hydrocarbon is
immature, not yet transformed into oil by natural processes, and are usually termed
"source rocks". Some adsorbed and some free gas may also exist.
Immature oil shales require a specialized log analysis model because the
Archie saturation model is often inappropriate.
Immature oil shale can be mined on the surface or
at depth and the rock heated in a retort to convert the organic
content to oil. Some valuable by products such as vanadium may
also be extracted, but dry clay, ash, and other minerals are a
serious waste disposal issue. In-situ extraction using
super-heated steam, air, carbon dioxide, or some other heat
transfer system is used to convert the organic carbon to oil.
Collector wells then extract the oil.
Immature oil shales have been exploited since the mid 1800's. An
interesting radio show gives a brief history and an over-hyped
future for the Colorado -Utah-Wyoming immature oil shales as
seen from the post-war perspective of 1946. Click
HERE to listen.
You can fast-forward over the first 5 minutes to avoid some
really bad scene-setting dialogue. And they "forgot" to mention
that Canada was the first to commercially produce kerosene from
shale oil in 1846.
 CLASSIFYING OIL Shale
CLASSIFYING OIL Shale
Immature oil shale has received many
different names over the years, such as cannel coal, boghead
coal, alum shale, stellarite, albertite, kerosene shale,
bituminite, gas coal, algal coal, wollongite, schistes
bitumineux, torbanite, and kukersite. Some of these names are
still used for certain types of oil shale. Recently, however,
attempts have been made to systematically classify the many
different types of oil shale on the basis of the depositional
environment of the deposit, the petrographic character of the
organic matter, and the precursor organisms from which the
organic matter was derived.
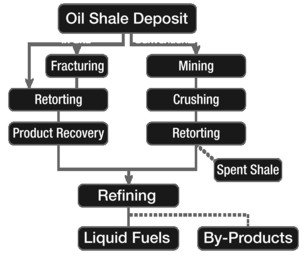
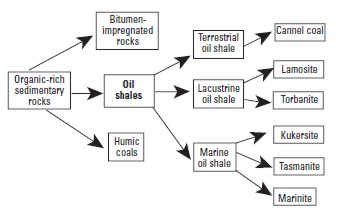
Flowchart for extracting oil from immature oil shale
Oil shale classification chart
A
useful classification of oil shales was developed by A.C.
Hutton. He divided oil shale into three groups based on their
deposition environment: terrestrial, lacustrine, and marine, and
further by the origin of their organic matter.
Terrestrial oil shales include those
composed of lipid-rich organic matter such as resin spores, waxy
cuticles, and corky tissue of roots and stems of vascular
terrestrial plants commonly found in coal-forming swamps and
bogs. Lacustrine oil shales include organic matter derived from
algae that lived in fresh, brackish, or saline lakes. Marine oil
shales are composed of organic matter derived from marine algae
unicellular organisms, and marine dinoflagellates.
  Resistivity image log in lacustrine
oil shale. White is high resistivity, Resistivity image log in lacustrine
oil shale. White is high resistivity,
black is low resistivity.
Within
these three groups, Hutton recognized six specific oil-shale
types, as shown in the diagram above:
1. Cannel coal is
brown to black oil shale composed of resins, spores, waxes, and
cutinaceous and corky materials derived from terrestrial
vascular plants together with varied amounts of vitrinite and
inertinite. Cannel coals originate in oxygen-deficient ponds or
shallow lakes in peat-forming swamps and bogs.
2. Lamosite is pale, grayish-brown and dark gray to black oil
shale in which the chief organic constituent is lamalginite
derived from lacustrine planktonic algae. Other minor components
include vitrinite, inertinite, telalginite, and bitumen. The
Green River oil-shale deposits in western United States and a
number of the Tertiary lacustrine deposits in eastern
Queensland, Australia, are lamosites.
3. Marinite is a gray to dark gray to black oil shale of
marine origin in which the chief organic components are
lamalginite and bituminite derived chiefly from marine
phytoplankton. Marinite may also contain small amounts of
bitumen, telalginite, and vitrinite. Marinites are deposited
typically in epeiric seas such as on broad shallow marine
shelves or inland seas where wave action is restricted and
currents are minimal. The Devonian–Mississippian oil shales of
eastern United States are typical marinites. Such deposits are
generally widespread covering hundreds to thousands of square
kilometers, but they are relatively thin, often less than 100 m.
4. Torbanite, named
after Torbane Hill in Scotland, is a black oil shale whose
organic matter is composed mainly of telalginite found in fresh-
to brackish-water lakes. The deposits are commonly small, but
can be extremely high grade.
5. Tasmanite, named
from oil-shale deposits in Tasmania, is a brown to black oil
shale. The organic matter consists of telalginite derived
chiefly from unicellular algae of marine origin and lesser
amounts of vitrinite, lamalginite, and inertinite.
6. Kukersite, which
takes its name from Kukruse Manor near the town of Kohtla-Järve,
Estonia, is a light brown marine oil shale. Its principal
organic component is telalginite derived from green algae.
Kukersdite is the main type of oil shale in Estonia and westtern
Russiaa, and is burned instead of coal to generate
electricity in power plants.
 OIL Shale IN CANADA
OIL Shale IN CANADA
 Canada
produced some shale oil from deposits in New Brunswick in the
mid-1800's. The mineral was called
Albertite and was originally believed to be a form of coal. Canada
produced some shale oil from deposits in New Brunswick in the
mid-1800's. The mineral was called
Albertite and was originally believed to be a form of coal.
 Albert Mines, New Brunswick, in 1850's Albert Mines, New Brunswick, in 1850's
Later, the nature of
the mineral and its relation to the surrounding oil shale was
described correctly. Abraham Gesner used Albertite in his early
experiments to distill liquid fuel from coal and solid bitumen.
He is credited with the invention of kerosene in 1846, and built
a significant commercial distillery to provide lighting oil to
replace whale oil in eastern Canada and USA. In the 1880's,
shale oil was abandoned as a source of kerosene in favour of
distillation from liquid petroleum.
Canada's oil-shale deposits range from
Ordovician to Cretaceous age and include deposits of lacustrine
and marine origin in at least 20 locations across the country.
During the 1980s, a number of the deposits were explored by core
drilling. The oil shales of the New Brunswick Albert Formation,
lamosites of Mississippian age, have the greatest potential for
development. The Albert oil shale averages 100 l/t of shale oil
and has potential for recovery of oil and may also be used for
co-combustion with coal for electric power generation.
Marinites, including the Devonian Kettle Point Formation and the
Ordovician Collingwood Shale of southern Ontario, yield
relatively small amounts of shale oil (about 40 l/t), but the
yield can be doubled by hydroretorting. The Cretaceous Boyne and
Favel marinites form large resources of low-grade oil shale in
the Prairie Provinces of Manitoba, Saskatchewan, and Alberta.
Upper Cretaceous oil shales on the Anderson Plain and the
Mackenzie Delta in the Northwest Territories have been little
explored, but may be of future economic interest.
 Total Organic CARBON (TOC)
Total Organic CARBON (TOC)
 Organic
content is usually associated with shales or silty shales, and
is an indicator of potential hydrocarbon source rocks. High
resistivity with some apparent porosity on a log analysis is a
good indicator of organic content. Kerogen is the main source of
TOC; kerogen is usually radioactive (uranium salts) but the
quantity of radioactivity is not a good predictor of the
quantity of organic matter.. Organic
content is usually associated with shales or silty shales, and
is an indicator of potential hydrocarbon source rocks. High
resistivity with some apparent porosity on a log analysis is a
good indicator of organic content. Kerogen is the main source of
TOC; kerogen is usually radioactive (uranium salts) but the
quantity of radioactivity is not a good predictor of the
quantity of organic matter..
Oil
shales contain predominantly Type I kerogen, as opposed to coal and
coal bed methane reservoirs, which contain mostly Type III. Gas
shales contain mainly Type II kerogen.
Various
methods for quantifying organic content from well logs have been
published. The most useful approaches are based on density vs
resistivity and sonic vs resistivity crossplots. Other approaches
using core measured TOC versus log data, for example density or
sonic readings are also common. See TOC
Calculation for details.
 Determining OIL YIELD (Grade) of
Oil Shale FROM ROCK SAMPLES
Determining OIL YIELD (Grade) of
Oil Shale FROM ROCK SAMPLES
The grade of oil shale has been determined by many
different methods with the results expressed in a variety of
units. The heating value of the oil shale may be determined
using a calorimeter. Values obtained by this method are reported
in English or metric units, such as British thermal units (Btu)
per pound of oil shale, calories per gram (cal/gm) of rock,
kilocalories per kilogram (kcal/kg) of rock, megajoules per
kilogram (MJ/kg) of rock, and other units.
The heating value is useful for determining the quality of an
oil shale that is burned directly in a power plant to produce
electricity. Although the heating value of a given oil shale is
a useful and fundamental property of the rock, it does not
provide information on the amounts of shale oil or combustible
gas that would be yielded by retorting (destructive
distillation).
The grade of oil shale can be determined by measuring the yield
of oil of a shale sample in a laboratory retort. The method
commonly used in Canada and United States is called the modified
Fischer assay, first developed in Germany, then adapted by the
U.S. Bureau of Mines. The technique was subsequently
standardized as the ASTM Method D-3904-80. Some laboratories
have further modified the Fischer assay method to better
evaluate different types of oil shale and different methods of
oil-shale processing.
The standardized Fischer assay consists of heating a 100-gram
sample crushed to –8 mesh (2.38-mm mesh) screen in a small
aluminum retort to 500ºC at a rate of 12ºC per minute and held
at that temperature for 40 minutes. The distilled vapors of oil,
gas, and water are passed through a condenser cooled with ice
water into a graduated centrifuge tube. The oil and water are
then separated by centrifuging. The quantities reported are the
weight percent of shale oil, water, shale residue, and “gas plus
loss” by difference. Some organic matter is turned to char and
reported as part of the shale residue. As a result, this assay
may understate the amount of oil that might be recovered in a
commercial scale retort that continuously mixes the feedstock.
Oil yield is usually converted from mass fraction into US or
Imperial gallons per ton (gpt or gal/t) of rock. So much for
going metric! In Canada, oil yields are quoted in liters per
metric ton of rock (l/t).
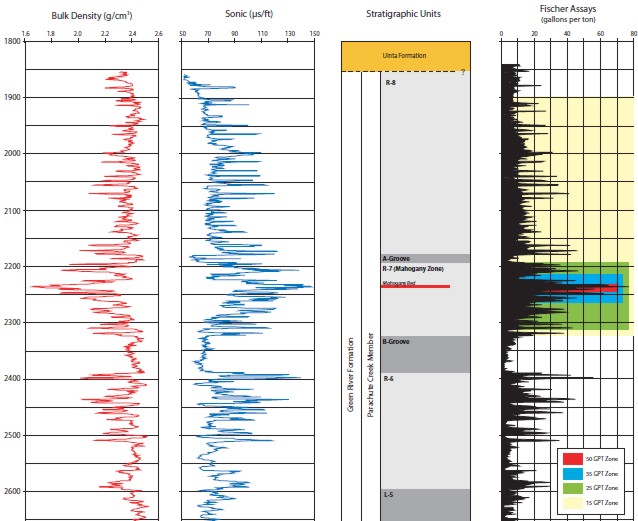
Oil shale example from Utah; density log (left), sonic (middle,
Fischer oil yield in gallons/ton (right). Note sonic scale is
reverse of conventional oilfield practice. Low density and high
sonic travel time correspond to high oil yield, analogous to
high porosity in conventional oilfield applications.
 Determining OIL YIELD (Grade) of
Oil Shale FROM WELL LOGS
Determining OIL YIELD (Grade) of
Oil Shale FROM WELL LOGS
Traditional methods for log analysis of oil
shales, dating back to the early 1960's, are somewhat
over-simplified regression methods using sonic or density data.
See for example "Evaluating Oil Shales by Well Logs" by S. R.
Bardsley and S. T. Aigermissen, AIME, 1962.
By crossplotting Fischer assay oil yields with corresponding
log data, regression lines are generated that provide a decent
average oil yield from logs. Problems related to matrix density
or matrix travel time variations due to mineral variations with
depth are masked by this method. Separate transforms are usually
taken when mineralogy is known to change. Logs average about 3
feet (1 meter) of rock compared to much finer detail available
from the core assay, so crossplots tend to show considerable
scatter in laminated intervals, as shown in the examples
below..
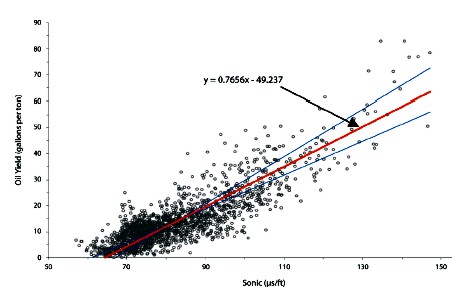  Sonic
log data versus oil yield from Utah example. Reduced major axis
best fit is the most appropriate regression method (red line).
Y-on-X and X-on-Y regression lines are also shown. Sonic is in
usec/foot, oil yield is in US gallons/ton (gpt or g/t)of rock. Sonic
log data versus oil yield from Utah example. Reduced major axis
best fit is the most appropriate regression method (red line).
Y-on-X and X-on-Y regression lines are also shown. Sonic is in
usec/foot, oil yield is in US gallons/ton (gpt or g/t)of rock.
Equation of the line is:
1: Y = 0.766 * DTC - 49.4
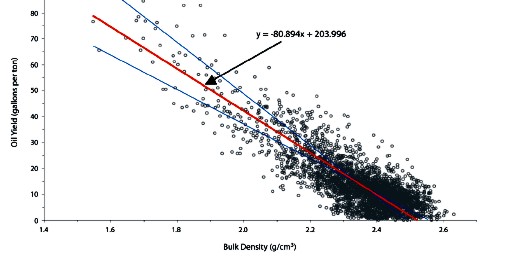
Density versus oil yield for
same data set. Density
is in grams/cc 
Equation of the line is:
2: Y = - 80.3 * DENS - 204
Data is from "Basin-Wide
Evaluation of Uppermost Green River Oil Shale Resources, Uinta
Basin, Utah and Colorado" by M. D. Vanden Berg, Utah Geol
Survey, 2008.
Equations for each individual well were also presented,
showing considerable variation from well to well and zone to
zone.
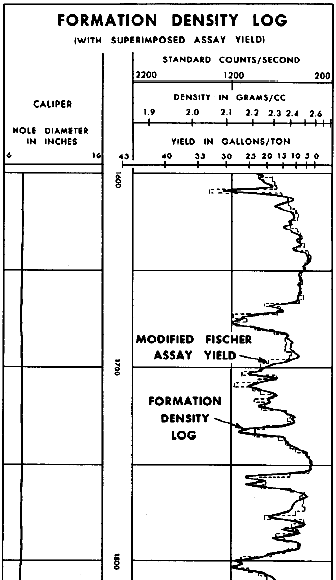
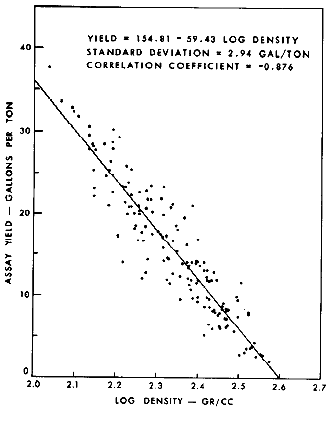
Portuib of debsity log with Fischer core assay (dashed
line) and crossplat of density and oil yield, from "Log
Evaluation of
Non-Metallic Minerals" SWSC, by M,P, Tixier and R.P/ Alger
 A
literature search quoted by R. M. Habiger and R. H. Robinson in
1985 gives the following equations for estimating oil yield: A
literature search quoted by R. M. Habiger and R. H. Robinson in
1985 gives the following equations for estimating oil yield:
Smith (1956) Garfield County, Colorado:
3: Y = 31.6 * DENS^2 - 206 * DENS + 327
4: Y = 22.9 * DENS^2 - 167 * DENS + 280
Bardsley and Algermissen (1963) Unita Basin, Utah:
5: Y = - 66.4 * DENS + 171
6: Y = 41.01x10^-4 = DTC^2 - 16.7
Tixier and Alger (1967) Piceance Basin, Colorado:
7: Y = - 59.4 * DENS + 155
Cleveland-Cliffs (1975) Uinta Basin, Utah
8: Y = 496 * DENS^-0.6 - 285
9: Y = 157 * 10^-4 * DTC^1.8 - 39.2
I have reduced all equations to 3 significant digits, which
is all that log analysis can support. The reader should refer to
the appropriate technical papers to see the data spread and
regional environment before using any of the above equations.
NUMERICAL EXAMPLE
DENS 2.2 1.8 g/cc
DTC 100 130 usec/ft
Smith
3: 26.7 58.6 US gal/ton
4: 23.4 53.6
Bardsley and Algermissen
5: 24.9 51.5
6: 24.3 52.6
Tixier and Alger
7: 24.3 48.1
Cleveland-Cliffs
8: 24.0 63.6
9: - 23.3 61.0
 MULTIPLE REGRESSION (PHILLIPS) METHOD
MULTIPLE REGRESSION (PHILLIPS) METHOD
A more sophisticated method was proposed by R. M. Habiger and R.
H. Robinson in 1985, using multiple linear regression of sonic,
density, and resistivity versus oil yield. The method was
patented by the authors on behalf of Phillips Petroleum (US
Patent #4548071), even though the method is strictly
mathematical and no "invention" was involved. The patent
actually claims to protect every individual step of the math,
including taking the logarithm of resistivity. Since
mathematical solutions and computer code cannot be patented,
infringement is moot. Both sonic and density crossplots of the
type shown above are included in the patent and in their 1985 SPWLA paper.
They were also faced with very poor quality density log data
from poorly calibrated slim hole, non-contact tools. As a
result, they had to normalize the density logs using histograms
and correlated density "variation" (DV) to oil yield instead of
raw density. DV was calculated from:
10: DV = DENSlog - DENSmean
This also had the effect of handling some of the matrix
density variations between wells, but not from layer to layer
within each interval in a single well.
A clay index was generated by regression:
11: CI = DTC + 127.31 * DV - 84.84
Their regression line is quoted as:
Upper zone:
12: Y = - 74.37 * DV + 7.86 * (log RESD) +
0.5 * CI - 9.65
Lower Zone
13: Y = - 81.58 * DV + 4.70 * (log RESD) + 9.36
Where"
DENSlog = actual log reading (gm/cc)
DENSmean = average density log readings over the analyzed interval
(gm/cc)
DV = density variation (gm/cc)
DTC = compressional sonic travel time (usec/ft)
CI = clay index (percent)
RESD = deep resistivity reading (ohm-m)
Y = oil yield (gallons per ton of rock).
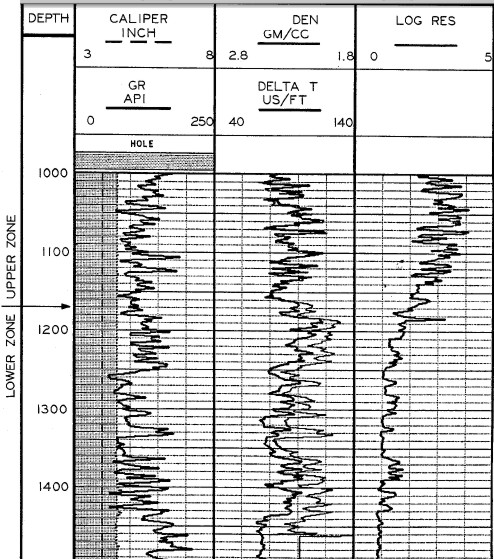
This is the log data from the paper and patent application.
Unfortunately neither
document contains an answer plot or Fischer assay data plotted
versus depth. Note that
both density and sonic scales are
reversed compared to normal oilfield practice.
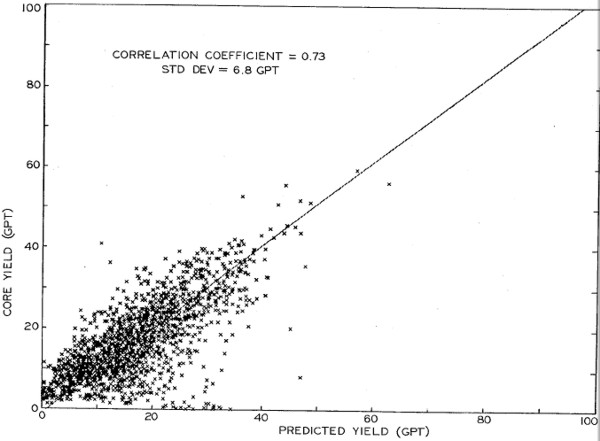
Comparison of Fischer assay oil yield versus yield
predicted from multiple regression.
 Multi-mineral models for
IMMATURE OIL SHALE evaluation
Multi-mineral models for
IMMATURE OIL SHALE evaluation
There are no good reasons to avoid
standard multi-mineral methods such as simultaneous equations,
principal components, or other statistical methods for oil
shales. Simultaneous equation solutions are widely used in
mineral evaluation from logs and are covered elsewhere in this
Handbook. A typical equation set for an oil shale would be:
14: DENS = 2.35 * Vshl + 2.65 * Vqtz + 2.74 * Vlim + 2.87 * Vdol
+ 0.95 * Vker
15: DTC = 120 * Vshl + 55 * Vqtz + 47 * Vlim + 44 *
Vdol + 200 * Vker
16: PHIN = 0.30 * Vshl - 0.05 * Vqtz + 0.00 * Vlim + 0.04 * Vdol
+ 0.95 * Vker
17: PE = 3.45 * Vshl + 1.85 * Vqtz + 5.10 * Vlim + 3.10 *
Vdol + 0.95 * Vker
18: 1.00 = Vshl + Vqtz + Vlim + Vdol + Vker
This equation set is inverted by
Cramer's Rule or with spreadsheet functions to obtain the
unknown volumes. Parameters must be adjusted to suit local
conditions. Minerals chosen must be guided by local knowledge,
based on petrography or XRD results. If a log curve is
unavailable or faulty due to bad hole conditions, the data can
be synthesized or the equation set reduced to eliminate that
curve, with the loss of one of the minerals in the answer set.
The volumetric results must then be converted
to mass fraction, as is done for tar sands, potash, and coal
analysis:
19: WTshl = Vshl * 2.35
20: WTqtz = Vqtz * 2.65
21: WTlim = Vlim * 2.71
22: WTdol = Vdol * 2.87
23: WTker = Vker * 0.95
24: WTrock = = WTshl + WTqtz + WTlms + WTdol + WTker
Mass fraction
25: Wker = WTker / WTrock
26: WT%ker = 100 * Wker
Where:
Vxxx = volume fraction of components
WTxxx = weight of components
Wxxx = mass fraction of components
WT%xxx = weight percent of components
Density parameters must match those used in the original simultaneous
equation set.
Kerogen mass fraction should be close to Oil Yield mass fraction from Fischer
analysis, or a simple linear conversion to account for "gas plus
loss". If Fischer analysis is given in US gal / ton or liters /
ton, suitable conversion factors must be used to obtain mass
fraction (ton / ton) for comparison to the log analysis results.
Calibration to Fischer assay data would permit adjustment of
parameters to produce a better match to core than is usual from
single or multiple regression. The core data should be averaged
over a 3 foot running average so that comparison to logs can be
more meaningful.
I have had no chance to test simultaneous or PCA approach
on oil shale, but have used it successfully in potash and
conventional multi-mineral oil reservoirs.
 META/LOG
"YIELD"
SPREADSHEET -- IMMATURE OIL SHALE ASSAY FROM LOG ANALYSIS META/LOG
"YIELD"
SPREADSHEET -- IMMATURE OIL SHALE ASSAY FROM LOG ANALYSIS
This
spreadsheet calculates an Oil Shale Assay that can be used to evaluate
oil shale quality and provides a comparison with Fischer core analysis
data.
SPR-17 META/-LOG SHALE OIL YIELD CALCULATOR
Calculate oil yield
in immature oil shale,
6 methods.

Sample output from "META/YIELD" spreadsheet for oil
shale qusality analysis.
 OIL SHALE EXAMPLE
OIL SHALE EXAMPLE
Raw data and computed results in an oil shale. Calculated oil
yield is in 2nd track from the right on a logarithmic scale of
1000 to 1.0 US gal/ton.
|






 Canada
produced some shale oil from deposits in New Brunswick in the
mid-1800's. The mineral was called
Albertite and was originally believed to be a form of coal.
Canada
produced some shale oil from deposits in New Brunswick in the
mid-1800's. The mineral was called
Albertite and was originally believed to be a form of coal.  Organic
content is usually associated with shales or silty shales, and
is an indicator of potential hydrocarbon source rocks. High
resistivity with some apparent porosity on a log analysis is a
good indicator of organic content. Kerogen is the main source of
TOC; kerogen is usually radioactive (uranium salts) but the
quantity of radioactivity is not a good predictor of the
quantity of organic matter..
Organic
content is usually associated with shales or silty shales, and
is an indicator of potential hydrocarbon source rocks. High
resistivity with some apparent porosity on a log analysis is a
good indicator of organic content. Kerogen is the main source of
TOC; kerogen is usually radioactive (uranium salts) but the
quantity of radioactivity is not a good predictor of the
quantity of organic matter..




 A
literature search quoted by R. M. Habiger and R. H. Robinson in
1985 gives the following equations for estimating oil yield:
A
literature search quoted by R. M. Habiger and R. H. Robinson in
1985 gives the following equations for estimating oil yield:



