|
 High
Resolution Dipmeter
High
Resolution Dipmeter
Four and six arm tools are less vulnerable to hole problems
than 3-arm tools. These
are called high resolution dipmeters. If one curve is unusable,
any three others may still be used to determine dip. Also, the
two (or three) independent sets of arms fit elliptical holes better.
For these reasons, four and six arm tools became the preferred
dipmeter in the 1970's and 80's.
Six
curve pair correlations can be attempted between four curves.
The adjacent curve pair displacements are designated respectively
as h12, h23, h34, and h41, and the diagonal displacements as h13
and h24. These six displacements can in turn be paired in thirteen
different ways to provide thirteen dip evaluations for the same
level. For the six arm dipmeter, 15 pairs are possible, leading
to additional redundancy. The result from each combination is
referred to as a dip determination. In recent practice, however,
only four or five correlations are made, leading to a maximum
of eight possible dip determinations per level. This reduces computer
time.
Four
arm closure error (Ec) is given by the algebraic sum of the four
adjacent curve displacements:
1: Ec = h12 + h23 + h34 + h41
For
perfect closure, Ec = 0.
Three
arm closure error can also be computed on a four arm or six arm
dipmeter. In this case, closure error is given by the algebraic
sum of two adjacent curve displacements and their associated diagonal
displacement. This error is distributed around the displacements
in proportion to the amount of each displacement.
When four or six arm closure exists, or has been created by distributing
the error, another error, the planarity error can be measured
among the four adjacent curve displacements. Because opposite
pairs of pads in the four pad array form a parallelogram, the
displacement observed between curves 1 and 2 should be the same
as that between curves 4 and 3, and the displacement between curves
2 and 3 should be equal to that between curves 1 and 4. Thus,
for perfect planarity:
2: h12 = -h34 and h23 = -h41
When
four arm closure error is zero, planarity error (Ep) is defined
as:
3: Ep = h12 + h34 - h23 - h41
For
perfect planarity, Ep = 0. Similar equations exist for the six
arm dipmeter.
If
closure error is zero and planarity is not zero, then several
things may be possible. One is that the bedding may not be planar,
such as in the case of festoon current bedding or aeolian dune
surfaces. Other possibilities are lack of pad contact with the
hole wall and possible miscorrelations. The latter are,
in fact, quite likely.
The
flow chart below shows the complex logic involved in
Schlumberger's high resolution dipmeter program. It handles the
closure and planarity problems in numerous ways, based on the
number and quality of correlations found.
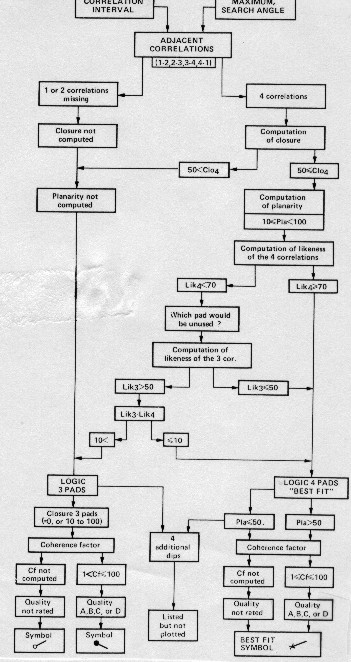
Dipmeter computation flowchart
The output listing from this program is shown below. Notice that
some of the logic choices are coded on the listing and others on
the arrow plot by use of alternate symbols.
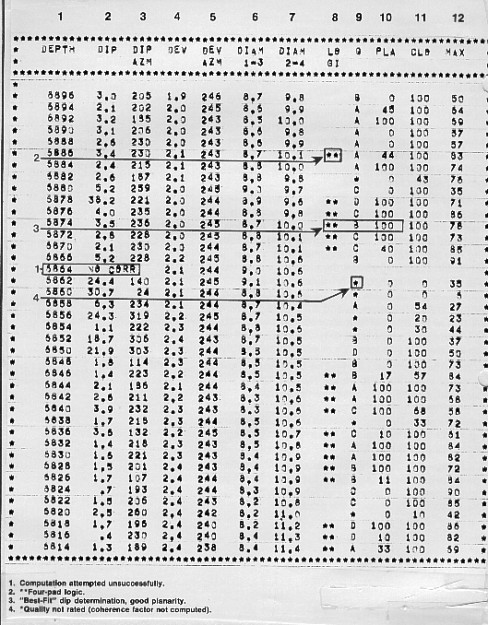
SHDT dipmeter computation output listing
Dips
can also be coded and presented in such a way as to indicate the
fact that they are non-planar. This would help an analyst interpret
the bedding, as shown in the example below, which was
processed using Gearhart's OMNIDIP program.
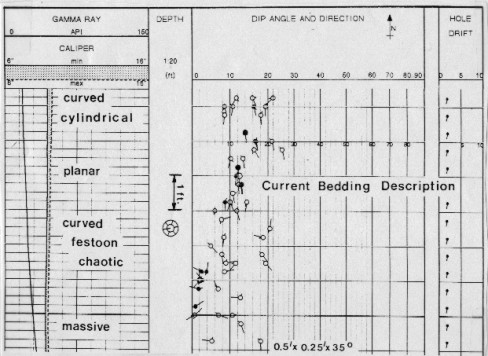
Coding non-planar dips helps interpret sedimentary
bedding
|

