|
 Basic 3 - arm Continuous Dipmeter Calculations
Basic 3 - arm Continuous Dipmeter Calculations
This Section deals
with the 3 arm dipmeter calculations that were performed in
the early days of dipmeter logging. These tools are no
longer run but the dip data can be found in well files. To
use that information, it pays to know how the calculations
were made and their limitations.
The computation of
early dipmeter data has been handled in one of three
general ways: manual processing, combination of manual and computer
processing, and total computer processing.
Manual
correlation and computation methods were developed first and there
are several different methods of doing the work. The dipmeter
curves must first be correlated; this may be done by slipping
a print of a log under the film used to make the print and measuring
the depth displacement between peaks and valleys on the curves.
Pad number one is used as a reference to measure displacements
to each of the other curves.
Another
method of curve correlation uses an optical comparator, a system
of mirrors and lenses which allow the user to optically lay one
curve over another and shift it up and down. The amount of shift
is measured mechanically on a dial and is recorded as the displacement.
After
these correlations have been made, the azimuth of the number one
electrode, the borehole deviation angle, the relative bearing,
and the borehole diameter from the calipers are recorded. This
information, plus the depth, is necessary to compute the dip angle
and dip direction of a point referenced to magnetic north. Because
true dip is referenced to true north, we must also account for
magnetic declination of the region.
Mathematical
formulas to solve this geometric puzzle are given later in this
Chapter. The manual calculation of dip magnitude and direction
with the above information was made in several ways: by using
a calculator and trigonometric tables, a scientific programmable
calculator (after 1970) with trig functions, a mathematically
derived physical computing device (in other words, an analog computer),
or stereographic nets, the latter being the most common manual
method used in the past. A very small amount of hand calculator
work is still done today.
Another
method of dipmeter computation utilized manual correlation and
computer reduction of the data. This type of processing was originally
developed to minimize turnaround time and to allow the tedious,
time consuming computation and plotting of results to be performed
by a digital computer. This may still be done today for re-computation
of continuous dipmeters recorded on paper, or on 7 track digital
tapes (which are unreadable by most modern computers) for which
the paper records are still available.
The
most recently developed system of computation is computer correlation
and calculation from data on digital magnetic tape. The data from
the magnetic tape is entered into a digital computer and processed.
In the correlation program, the digital information representing
the dipmeter curves is stored in memory and the data from one
trace is compared to the other traces to determine the vertical
displacement between the traces. After these displacements are
calculated, the tool orientation information is used to compute
the actual formation dips.
The
standard correlation process is performed by a mathematical function
called cross-correlation, in which the offset distance between
events on two curves are found. The distance between the center
and the maximum amplitude on the correlagram indicates the displacement
between the two curves. The offsets for all curve pairs are then
adjusted to obtain the offsets relative to the center of the correlation
interval. More exotic forms of correlation, some based on pattern
recognition theory, are used in the newer programs.
The
length of the portion of the curve being correlated is called
the correlation interval, correlation length, or correlation window.
Correlation interval is usually between one and four feet, but
can be smaller or larger. The correlation is calculated at regular
intervals along the log. The distance between correlations is
called the step distance and is usually 1/2 to 1/4 of the correlation
interval. One dip value is calculated at the center of each correlation
window, and the dip value is plotted at each step distance.
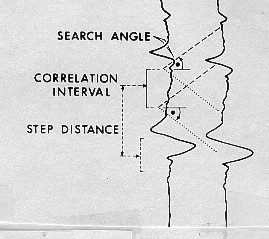 In
order to determine how far up and down each adjacent curve the
correlation is to be performed, a search angle is defined. In
moderate structural dip the search angle is usually 45 degrees,
but if expected dips are low, the angle can be reduced to
eliminate noise, or spurious dips caused by erratic wiggles on
the curves. Some computer programs use a search length instead
of a search angle. In steep dips, a higher search angle is
required. These terms are illustrated at the right. In
order to determine how far up and down each adjacent curve the
correlation is to be performed, a search angle is defined. In
moderate structural dip the search angle is usually 45 degrees,
but if expected dips are low, the angle can be reduced to
eliminate noise, or spurious dips caused by erratic wiggles on
the curves. Some computer programs use a search length instead
of a search angle. In steep dips, a higher search angle is
required. These terms are illustrated at the right.
Dipmeter computation definitions
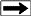
The
number of dips computed from computer processed logs can be any
density required for a particular purpose. For structural analysis,
normal densities range from one computation every one or two feet
to one computation every ten feet. In those instances where additional
information is required, such as for stratigraphic analysis, points
as close as every few inches can be computed.
The
usual way to describe these parameters is in the form CORR x STEP
x ANGLE. For example a 4 x 1 x 45 process uses a 4 foot correlation,
a 1 foot step, with a 45 degree search angle. The recommended
defaults for dipmeter processing are:
Low
angle structural dip: 4 x 2 x 45 eg: normal or reverse faults,
folds
High
angle structural dip: 8 x 4 x 80 eg: overthrust faults, recumbent
folds
Sand
body stratigraphic dip: 2 x 1 x 30 eg: beach, bar, channel, drape
Complex
stratigraphic dip: 1 x 0.5 x 30 eg: submarine fan, scree slope,
turbidite
A
fourth parameter is sometimes used to indicate that the program
can search farther up the curve if no correlation is found. This
is shown as:
4 x 2 x 35 x 2
which allows the program to use a 70 degree search angle after
failing at 35 degrees.
The
effect of a shorter correlation interval is shown below, where only regional dip is found in the long interval
case, and stratigraphic dip is superimposed on the regional when
a short interval is used.
Regional and stratigraphic dipmeter computation
using different correlation interval
The
problem with dip determination by cross-correlation is that it
does average all dips found in the correlation interval. If both
structural and stratigraphic dips are present, the average may
not reflect either of them correctly, regardless of the correlation
interval. Regional dip is therefore usually chosen in a nearby
shale or bedded carbonate thick enough to give an accurate result,
without interference from stratigraphic events.
Many
dipmeters have been computed with inappropriate parameters and
could be improved by re-computation with a better choice of values.
The defaults shown above are just starting points. In particular,
parameters for steeply deviated holes may need considerable experimentation
and variation throughout the hole.
To compute the displacements between the wiggles on a three curve
continuous dipmeter, we could correlate at each computation level,
defined by the correlation length, a segment of curve 1 with curve
2 first, and then correlate a segment of curve 2 with curve 3.
The two displacements found would be sufficient to determine the
dip. However, we might just as well have correlated curves 2 and
3 then curves 3 and 1, or curves 3 and 1 and then 1 and 2. All
three combinations of displacement pairs should in theory define
the same bedding plane, and the same dip. If they do not, a closure
error exists.
In
manual correlations, one could correlate three pairs, determining
three displacements. For perfect closure, the algebraic sum of
the displacements must be zero. Usually, because of the inaccuracy
of the optical comparator, a small closure error existed. This
error could then be distributed among the three displacements
as a small correction before final determination of the dip. In
practice, this was an onerous task, and two pairs were often picked
with no attempt to determine closure error.
In
automatic correlations, two kinds of closure errors can occur:
small ones due to minor variations in shape between the three
curves, and large errors. Small errors are handled as for manual
computation.
When
a large error exists, it is because at least one of the correlations
is in error - the same geological event is not being picked on
all three pairs. In manual correlation, a large error was usually
fixed by re-picking one of the correlated curves. For an automatic
computation, we have to choose between three possible computable
dips, only one of which may be correct. There are no strong mathematical
rules to choose the correct dip. If closure error is large, the
usual procedure is to compute no result and display no dip arrow.
The
three arm tool is also vulnerable to adverse hole conditions.
If one curve degenerates, for instance when one pad fails to make
a good contact with the borehole wall, the computation of dip
cannot be made at all. This happens often in deviated holes or
in out-of-round holes, resulting in more intervals with no result.
|

