|
 CORE POROSITY BASICS
CORE POROSITY BASICS
Porosity is an intrinsic property of reservoir
rocks and indicates the storage capacity of the reservoir.
It is used as a primary indicator of reservoir quality, and
along with a few other factors, to calculate
hydrocarbon volume in place, and recoverable reserves. Petrophysicists use core porosity values to help calibrate
porosity derived from well log data.
 CORE POROSITY DEFINITIONS
CORE POROSITY DEFINITIONS
Porosity is the volume of the portion of the rock filled
with fluids, divided by the total volume of the rock. It is
usually abbreviated with Greek letter PHI, with subscripts
to indicate the porosity type, eg. PHIt, PHIe, PHIsec.
Primary porosity is the porosity developed by the original sedimentation
process by which the rock was created. In reports, it is often
referred to in terms of percentages, while in calculations it
is always a decimal fraction.

Secondary porosity is created by processes other than primary
cementation and compaction of the sediments. An example of secondary
porosity can be found in the solution of limestone or dolomite
by ground waters, a process which creates vugs or caverns. Fracturing
also creates secondary porosity. Dolomitization results in the
shrinking of solid rock volume as the material transforms from
calcite to dolomite, giving a corresponding increase in porosity.
In the laboratory, porosity is usually derived from easily
made measurements such as weight and volume. Here are the
definitions needed:
* Vg = grain volume
* Vp = pore volume
* Vb = bulk volume of a rock = Vg + Vp
* PHIcore = core porosity = Vp / Vb
OR:
* PHIcore = = core porosity = (Vb - Vg) / Vb
Notes:
"V" in this Chapter stands for Volume, not
Velocity.
These volumes are usually reported in cubic
centimeters (cc).
PHIcore may be close to total porosity (PHIt) or effective
porosity (PHIe) or somewhere in-between, depending on the core
analysis method and the details of how that method was applied.
The properties Vb, Vg, and Vp can be measured in the lab on full diameter core or on
smaller core plugs drilled from the whole core, or from sidewall
percussion or sidewall rotary cores. Whole core is best in
heterogeneous reservoirs and in low porosity reservoirs.
 MEASURING BULK VOLUME (Vb)
MEASURING BULK VOLUME (Vb)
There are 3 ways to measure bulk volume:
s. direct measurement of the dimensions of a
regular solid
b. fluid displacement using Archimedes Principle
c. fluid displacement using calibrated container
(pycmometer)
 DIRECT MEASUREMENT: Bulk Volume = Pi * Length * Radius
squared
DIRECT MEASUREMENT: Bulk Volume = Pi * Length * Radius
squared
4: Vb = PI * L * D^2 / 4
This method is less accurate due to the roughness of the
surfaces of the solid and imperfections in shape.
 ARCHIMEDES METHOD
ARCHIMEDES METHOD
This
technique utilizes the Archimedes’ principle of mass
displacement in a liquid (buoyancy):
a. The core is first cleaned, dried,
and weighed in air (WTdry)
b. The core sample is then saturated
with a wetting fluid and weighed (WTsat)
(the core may be coated with paraffin to prevent evaporation)
c. The sample is then submerged in
the same fluid and its submerged weight is measured (WTsub)
d. The bulk volume is the difference
between the last two weights divided by the density of the fluid.
e. The porosity is the difference
between the first two weights divided by the density of the fluid.
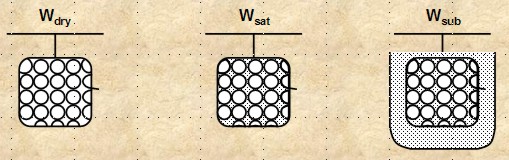
Bulk
Volume = (Weight in air (saturated) - Weight submerged) / Density of Fluid
5: Vb = (WTair - WTsub) / DENSfl
6: Vg = (WTdry - WTsub) / DENSfl
7: Vp = (WTsat - WTdry) / DENSfl
8: PHIt = (WTsat - WTdry) / (WTsat -
WTsub) = Vp / Vb
Bulk Density = Saturated Weight / Bulk Volume
9: BulkDens = WTsat / Vb
If clays are present and sample is maintained at a high humidity
(not over dried), this last equation gives PHIe, not PHIt.
Laboratory measurements using this technique are very accurate.
 CALIBRATED DISPLACEMENT METHOD
CALIBRATED DISPLACEMENT METHOD
The bulk volume can be determined also by the volume of the
displaced fluid. Fluids that
are normally used are water,
which can easily be evaporated afterwards, and mercury, which normally does not enter
the pore space in a core sample due to its non-wetting
capability and its large interfacial tension against air.
Bulk
Volume = Volume of Displaced Fluid = Weight Displaced Fluid /
Density Displaced Fluid
10: Vb = WTdisp / DENSfl
Laboratory measurements using this technique are very accurate.
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
WTdry = dry weight in air = 16.0 gm
WTsat = weight of saturated sample in air = 20.0 gm
WTcoated = weight of dry sample coated with paraffin = 20.9 gm
(density of paraffin = 0.9 gm/cc)
WTsub = weight coated sample immersed in water at 70 °F = 10 gm
(density of water = 1.0 gm/cc)
Determine bulk volume
Weight of paraffin = WTcoated - WTsar = 20.9 -
20.0 = 0.9 gm
Density of Parrafin = 0.9 gm/cc
Volume of paraffin = WTpar / DENSpar = 0.9 / 0.9 = 1.0 cc
Weight of water displaced = WTcoated - Wtsub = 20.9 - 10.0 =
10.9 gm
Volume of water displaced = 10.9 / 1.0 = 10.9 cc
Volume of water minus displaced-volume of
paraffin = 10.9 - 1.0 = 9.9 cc
Bulk volume of rock = 9.9 cc
 MEASURING GRAIN VOLUME (Vg) MEASURING GRAIN VOLUME (Vg)
There are 3 ways to measure grain
density in the lab:
a. assume a grain density, compare to
dry weight
b. displaced fluid method
c. Boyle's Law
 ASSUMED GRAIN DENSITY
ASSUMED GRAIN DENSITY
Determine Vg from the dry weight of the sample and the
rock grain density (2.65 gm/cc for quartz grains). This method
is not very accurate if grain density varies due to varying
mineralogy.
Grain Volume =
Dry Sample Weight / Grain Density
11: Vg = WTdry / DENSMA
 DISPLACED FLUID METHOD
DISPLACED FLUID METHOD
A more accurate approach is to use the displaced fluid
volume. First the core plug is measured to obtain its bulk
volume, as described earlier Then the sample is crushed to eliminate all porosity and
weighed (WTgr). A glass tube filled with water, called a pycnometer to
confuse novices, is weighed (W1), then the crushed rock is placed in
the tube (still filled with water), and weighed again WT2). The
difference in weights gives the volume of displaced fluid.
Displaced
Volume = Crushed Sample Weight + Water-filled tube Weight
- Combined Weight
12: Vdisp = (WT2 - WT1)
Grain Volume = Displaced Volume /
Water Density
13: Vg = Vdisp / DENSwater
Porosity = (Bulk Volume - Grain
Volume) / Bulk Volume
14: PHIt = (Vb - Vg) ' Vb
If clays are present and sample is maintained at a high
humidity (not over dried), this last equation gives PHIe, not
PHIt.
Grain Density = Dry Weight in Air / Grain Volume
15: GrainDens = WTdry / Vg
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
WTdry = Weight of dry crushed sample in air = 16.0 gm,
WT1 = Weight of pycnometer filled with water at 70 °F =
65.0 gm
WT2 = Weight of pycnometer filled with water and crushed sample
= 75.0 gm
Calculate grain volume
Volume of water displaced = 16.0 + 65.0 - 75.0 = 6.0 gm
Grain Volume = 6.0 / 1.0 = 6.0 cc
Calculate porosity
Bulk volume of the sample = 9.9 cc, from previous example
Total porosity = (9.9 - 6.0) / 9.9 = 0.394 fractional
porosity (39.4%)
 BOYLE'S LAW METHOD
BOYLE'S LAW METHOD
An
alternate grain volume method makes use of Boyle’s Law.
This gas
transfer technique involves the injection and decompression of
gas (Helium, CO2, or N2) into the pores of a fluid-free
(vacuum), dry core sample. Either the pore volume or the grain
volume can be determined, depending upon the instrumentation and
procedures.
To determine grain volume using ideal gas law at constant
temperature:
a. connect two cells of known volume, Vcell1 and Vcell2
b. close valve between cells, apply pressure P1 to cell 1
c. place dry core sample in cell 2, seal and evacuate cell 2
d. open valve and measure pressure P2
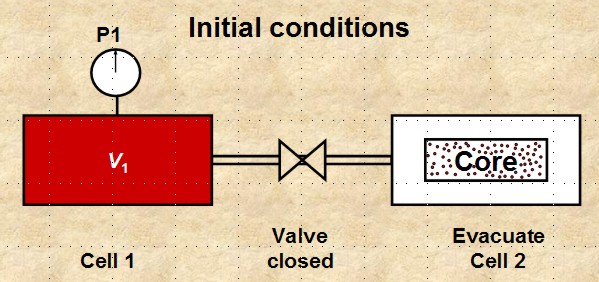
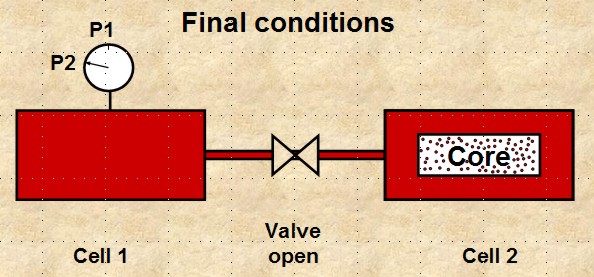
Boyle's Law apparatus to measure grain volume Vg
16: V2
= P1 * Vcell1 / P2
Since V2 = Vcell1 + Vcell2 - Vg And Vtotal = Vcell1 + Vcell2
Then 17: Vg = Vt - Vf
 MEASURING PORE VOLUME MEASURING PORE VOLUME
In previous sections pore volume Vp
was derived from volumetric methods based on weight and density.
Semi-direct measurement of porosity can also be attempted.
 BOYLE'S LAW METHOD
BOYLE'S LAW METHOD
Pore volume measurements can be done by using the Boyle’s Law
model, where the sample is placed in a rubber sleeve holder that
has no void space around the periphery of the core and on the
ends. Such a holder is called the Hassler holder, or a
hydrostatic load cell. Helium
or one of its substitutes is injected into the core plug through
the end stem.
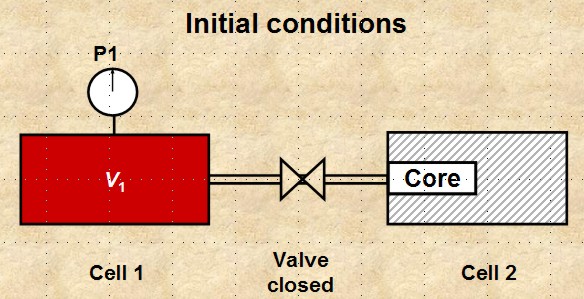
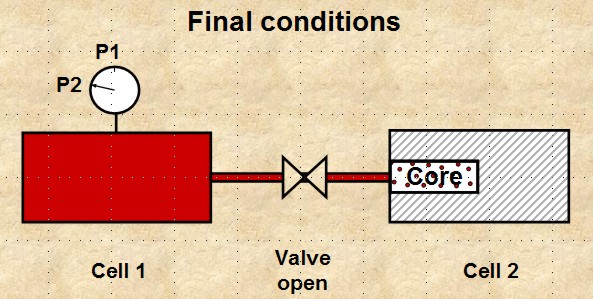
Boyle's Law apparatus for determining porosity
18: V2
= P1 * Vcell1 / P2
Since V2 = Vcell1 + PHIe
Then 19: Vp = V2 - Vcell1
 FLUID SUMMATIONS METHOD
FLUID SUMMATIONS METHOD
This technique is used to measure the volume of gas, oil and
water present in the pore space of a fresh or preserved
(peel-sealed) core of known bulk volume. The volumes of the
extracted oil, gas, and water are added to obtain the pore
volume and hence the core porosity.
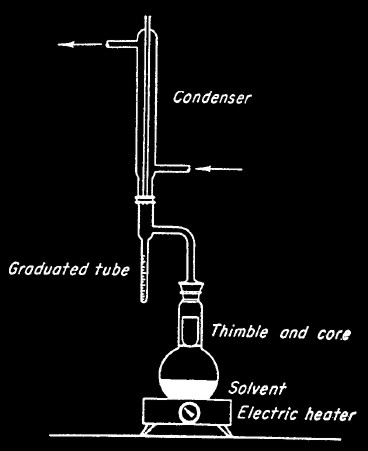
 DEAN-STARK CORE ANALYSIS METHOD
DEAN-STARK CORE ANALYSIS METHOD
This method is used in poorly consolidated rocks such as
tar samds and involves
disaggregating the samples and weighing their constituent
components. Samples are usually frozen or wrapped in plastic to
preserve the contents during transport. In the lab, the still
frozen cores are slabbed for photography and description, then
samples are selected and weighed.
Samples are then heated and crumbled to drive off water, and
weighed again. The weight loss gives the water weight. Solvents
are used to remove oil or tar. The sample is weighed again and
the weight loss is the weight of oil. The matrix rock is
separated into clay and mineral components by flotation, dried
and weighed again, giving the weight of clay and weight of the
mineral grains.
20: WTwtr = WTsample - WTheated
21: WTtar = WTheated - WTminerals&clay
 By dividing each weight by its respective density and
adjusting each result for the total weight of the sample, the
volume fraction of each is obtained. Porosity is the sum of
water plus oil volume fractions Because the bound water in
the clay is driven off by the drying sequences, this porosity is
the total porosity. By dividing each weight by its respective density and
adjusting each result for the total weight of the sample, the
volume fraction of each is obtained. Porosity is the sum of
water plus oil volume fractions Because the bound water in
the clay is driven off by the drying sequences, this porosity is
the total porosity.
22: VOLwtr = WTwtr / DENSwtr / WTsample
23: VOLtar = WTtar / DENStar / WTsample
24: PHIcore = VOLwtr + VOLtar
 Dean-Stark laboratory apparatus Dean-Stark laboratory apparatus
 Assuming clay bound water is driven off by heating and drying,
then PHIcore equals total porosity. From comparison to log
analysis results, it appears that some clay bound water remains
in many cases, so PHIcore lies between total and effective
porosity from log analysis. Assuming clay bound water is driven off by heating and drying,
then PHIcore equals total porosity. From comparison to log
analysis results, it appears that some clay bound water remains
in many cases, so PHIcore lies between total and effective
porosity from log analysis.
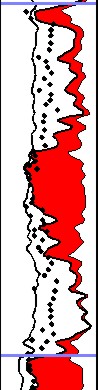
Example of Dean-Stark porosity (dots) showing that it is
less than total porosity
from logs (black curve) due to incomplete drying of clay. Trying to match
log
porosity directly to core may be futile in many cases. Scale is 0.50 to
0.00. 
 OIL MASS FROM CORE LISTINGS
OIL MASS FROM CORE LISTINGS
If not provided on the core listing, the equivalent value of tar mass from core analysis
is derived from porosity, oil saturation, and an assumed oil
density:
25: Wtar = PHIcore * Star * DENStar
26: Wwtr = PHIcore * Swtr * DENSwtr
27: Wrock = (1 – PHIcore) * GR_DENScore
Where:
Star = tar volume relative to pore volume
Swtr = water volume relative to pore volume
PHIcore = volume of water + valume of tar
Wtar = tar mass fraction
Wwtr = water mass fraction
Wrockcore = rock mass fraction
|
PHIcore |
Soil |
Swtr |
Vol Tar |
Vol Wtr |
GR_ DEN |
WT Oil |
WT Sand |
WT Wtr |
WT Rock |
Oil Mass Wtar |
Wtr Mass Wwtr |
Rock Mass Wrock |
|
frac |
frac |
frac |
frac |
frac |
kg/m3 |
|
|
|
|
frac |
frac |
frac |
|
0.306 |
0.301 |
0.699 |
0.092 |
0.214 |
2.650 |
0.092 |
1.839 |
0.212 |
2.143 |
0.043 |
0.099 |
0.858 |
|
0.271 |
0.236 |
0.764 |
0.064 |
0.207 |
2.650 |
0.064 |
1.932 |
0.207 |
2.203 |
0.029 |
0.094 |
0.877 |
|
0.279 |
0.306 |
0.694 |
0.085 |
0.194 |
2.650 |
0.085 |
1.911 |
0.193 |
2.189 |
0.039 |
0.088 |
0.873 |
|
0.244 |
0.304 |
0.696 |
0.074 |
0.170 |
2.650 |
0.074 |
2.003 |
0.168 |
2.246 |
0.033 |
0.075 |
0.892 |
|
0.298 |
0.217 |
0.783 |
0.065 |
0.233 |
2.650 |
0.065 |
1.860 |
0.233 |
2.158 |
0.030 |
0.108 |
0.862 |
|
0.273 |
0.298 |
0.702 |
0.081 |
0.192 |
2.650 |
0.081 |
1.927 |
0.191 |
2.199 |
0.037 |
0.087 |
0.876 |
If saturations (or pore volume) are
known, as well as core porosity, all other terms can be calculated.
Some core analysis reports do the math for you, some do not.
Since GR_DENScore represents a mixture of quartz and
shale, this value should vary with shale volume. However shale
volume is never reported on core analysis, so the composite grain
density from the rock sample is used. If grain density is
not recorded in the core analysis, we must assume a constant of 2650 kg/m3 or lower.
 FLUID VOLUMES FROM CORE LISTINGS
FLUID VOLUMES FROM CORE LISTINGS
If not provided on the core listing, the equivalent value of tar
volumes from core analysis
are derived from porosity, tar mass fraction, and an assumed oil
density:
27: Star = Wtar / (PHIcore * DENStar)
28: Swtr
= Wwtr / (PHIcore * DENSwtr)
OR 29: Swtr = 1.00 - Star
Where:
Star = tar volume relative to pore volume
Swtr = water volume relative to pore volume
PHIcore = volume of water + valume of tar
Wtar = tar mass fraction
Wwtr = water mass fraction
|
PHIcore |
Star |
Swtr |
Vol Oil |
Vol Wtr |
GR_ DEN |
WT Tar |
WT Sand |
WT Wtr |
WT Rock |
Tar Mass Wtar |
Wtr Mass Wwtr |
Rock Mass Wrock |
|
frac |
frac |
frac |
frac |
frac |
kg/m3 |
|
|
|
|
frac |
frac |
frac |
|
0.306 |
0.301 |
0.699 |
0.092 |
0.214 |
2.650 |
0.092 |
1.839 |
0.212 |
2.143 |
0.043 |
0.099 |
0.858 |
|
0.271 |
0.236 |
0.764 |
0.064 |
0.207 |
2.650 |
0.064 |
1.932 |
0.207 |
2.203 |
0.029 |
0.094 |
0.877 |
|
0.279 |
0.306 |
0.694 |
0.085 |
0.194 |
2.650 |
0.085 |
1.911 |
0.193 |
2.189 |
0.039 |
0.088 |
0.873 |
|
0.244 |
0.304 |
0.696 |
0.074 |
0.170 |
2.650 |
0.074 |
2.003 |
0.168 |
2.246 |
0.033 |
0.075 |
0.892 |
|
0.298 |
0.217 |
0.783 |
0.065 |
0.233 |
2.650 |
0.065 |
1.860 |
0.233 |
2.158 |
0.030 |
0.108 |
0.862 |
|
0.273 |
0.298 |
0.702 |
0.081 |
0.192 |
2.650 |
0.081 |
1.927 |
0.191 |
2.199 |
0.037 |
0.087 |
0.876 |
If oil mass fraction and water mass
fraction are known, as well as core porosity, all other terms can be
calculated. Some core analysis reports do the math for you, some do
not.
 POROSITY FROM
MICRO CT SCANS
POROSITY FROM
MICRO CT SCANS
Porosity is directly calculated from
high resolution digital images such
as those shown below. This
calculation is the ratio of the
number of voxels that fall into the
pore space (black and dark-gray) to
the total number of voxels in a 3D
image. The task of separating the
pores from grains in such 3D objects
is called image segmentation.
The main technical challenge in
image segmentation is the gradual
transition from dark to light shade
of gray at the edges of the pore
space. Proprietary image-processing
algorithms are used, which
include statistical analysis of the
gray-scale images. As a result, the
pore space is accurately separated
from the mineral matrix and the
porosity is computed. Source:
www.ingrainrocks.com.



Clean sand 39%
Tight sand 5%
Poorly sorted 12%
Silty Shale 8%
Black = Porosity, Grey =
Matrix Grains, White = Heavy
Minerals
 SAMPLE CORE ANALYSIS REPORT SAMPLE CORE ANALYSIS REPORT
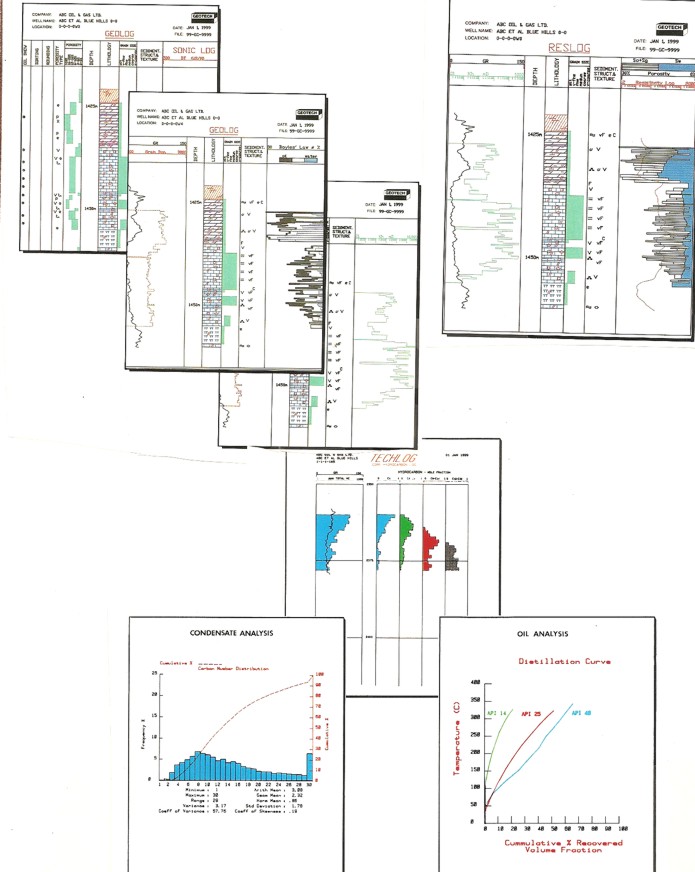
Samples of core analysis and core description plots, with a few
of the posible histograms and crossplots that can be made.
|
02181815W4 |
#23708 |
731011 |
|
NOTE: Accumap has Kvert in K90 Column |
|
S# |
Top |
Base |
Len |
Kmax |
K90 |
Kvert |
Poros |
GrDen |
BkDen |
Soil |
Swtr |
Lithology |
|
|
feet |
feet |
feet |
mD |
mD |
mD |
Frac |
kg/m3 |
kg/m3 |
frac |
frac |
|
|
1 |
3499.19 |
3500.17 |
0.98 |
742.0 |
0.0 |
180.0 |
0.283 |
0 |
0 |
0.129 |
0.448 |
SS VF-F |
|
2 |
3500.17 |
3501.16 |
0.98 |
1196.0 |
0.0 |
694.0 |
0.297 |
0 |
0 |
0.123 |
0.450 |
SS VF-F |
|
3 |
3501.16 |
3502.17 |
1.02 |
622.0 |
0.0 |
266.0 |
0.276 |
0 |
0 |
0.111 |
0.520 |
SS VF-F |
|
4 |
3502.17 |
3503.16 |
0.98 |
223.0 |
0.0 |
50.5 |
0.271 |
0 |
0 |
0.129 |
0.479 |
SS VF-F |
|
5 |
3503.16 |
3503.88 |
0.72 |
837.0 |
0.0 |
171.0 |
0.278 |
0 |
0 |
0.110 |
0.504 |
SS VF-F PY |
|
6 |
3503.88 |
3504.57 |
0.69 |
407.0 |
0.0 |
113.0 |
0.287 |
0 |
0 |
0.118 |
0.466 |
SS VF-F |
|
7 |
3504.57 |
3504.67 |
0.10 |
|
0.0 |
0.0 |
0 |
0 |
0 |
0 |
0 |
SH |
|
8 |
3504.67 |
3505.26 |
0.59 |
514.0 |
0.0 |
365.0 |
0.253 |
0 |
0 |
0.151 |
0.398 |
|
|
9 |
3505.26 |
3505.49 |
0.23 |
100.0 |
0.0 |
2.6 |
0.201 |
0 |
0 |
0.134 |
0.358 |
SS VF-F SH INC |
|
10 |
3505.49 |
3505.98 |
0.49 |
401.0 |
0.0 |
120.0 |
0.254 |
0 |
0 |
0.143 |
0.268 |
SS VF-F SHBKS |
|
11 |
3505.98 |
3506.96 |
0.98 |
478.0 |
0.0 |
302.0 |
0.282 |
0 |
0 |
0.131 |
0.471 |
SS VF-F |
|
12 |
3506.96 |
3507.88 |
0.92 |
431.0 |
0.0 |
100.0 |
0.243 |
0 |
0 |
0.156 |
0.399 |
SS VF-F CARB INC |
|
13 |
3507.88 |
3508.47 |
0.59 |
777.0 |
0.0 |
556.0 |
0.277 |
0 |
0 |
0.119 |
0.389 |
SS VF-F |
|
14 |
3508.47 |
3508.87 |
0.39 |
831.0 |
0.0 |
383.0 |
0.275 |
0 |
0 |
0.136 |
0.422 |
SS VF-F CARB BK |
|
15 |
3508.87 |
3509.88 |
1.02 |
413.0 |
0.0 |
262.0 |
0.281 |
0 |
0 |
0.132 |
0.440 |
SS VF-F |
|
16 |
3509.88 |
3510.87 |
0.98 |
604.0 |
0.0 |
425.0 |
0.277 |
0 |
0 |
0.131 |
0.323 |
SS VF-F SH INC |
|
17 |
3510.87 |
3511.88 |
1.02 |
320.0 |
0.0 |
35.1 |
0.229 |
0 |
0 |
0.146 |
0.422 |
SS VF-F SH INC |
|
18 |
3511.88 |
3512.87 |
0.98 |
616.0 |
0.0 |
437.0 |
0.239 |
0 |
0 |
0.103 |
0.354 |
SS VF-F |
|
19 |
3512.87 |
3513.79 |
0.92 |
259.0 |
0.0 |
62.0 |
0.261 |
0 |
0 |
0.073 |
0.418 |
SS VF-F |
|
20 |
3513.79 |
3514.38 |
0.59 |
320.0 |
0.0 |
26.8 |
0.219 |
0 |
0 |
0.096 |
0.441 |
|
|
21 |
3514.38 |
3515.07 |
0.69 |
431.0 |
0.0 |
82.5 |
0.236 |
0 |
0 |
0.119 |
0.387 |
SS VF-F |
|
22 |
3515.07 |
3515.16 |
0.10 |
|
0.0 |
0.0 |
|
|
|
|
|
SH PY |
|
23 |
3515.16 |
3516.18 |
1.02 |
969.0 |
0.0 |
628.0 |
0.270 |
0 |
0 |
0.044 |
0.492 |
SS VF-F |
|
24 |
3516.18 |
3516.77 |
0.59 |
837.0 |
0.0 |
634.0 |
0.280 |
0 |
0 |
0.042 |
0.501 |
SS VF-F |
|
25 |
3516.77 |
3517.46 |
0.69 |
556.0 |
0.0 |
201.0 |
0.273 |
0 |
0 |
0.050 |
0.531 |
SS VF-F CARB INC |
|
26 |
3517.46 |
3518.28 |
0.82 |
706.0 |
0.0 |
338.0 |
0.262 |
0 |
0 |
0.046 |
0.487 |
SS VF-F |
|
27 |
3518.28 |
3519.07 |
0.79 |
502.0 |
0.0 |
377.0 |
0.238 |
0 |
0 |
0.079 |
0.494 |
SS VF-F CARB INC |
|
28 |
3519.07 |
3519.99 |
0.92 |
1136.0 |
0.0 |
183.0 |
0.263 |
0 |
0 |
0.063 |
0.501 |
SS VF-F |
|
29 |
3519.99 |
3520.58 |
0.59 |
825.0 |
0.0 |
291.0 |
0.265 |
0 |
0 |
0.052 |
0.563 |
|
|
30 |
3520.58 |
3521.46 |
0.89 |
1346.0 |
0.0 |
706.0 |
0.274 |
0 |
0 |
0.055 |
0.516 |
SS VF-F |
|
31 |
3521.46 |
3522.48 |
1.02 |
389.0 |
0.0 |
102.0 |
0.246 |
0 |
0 |
0.064 |
0.450 |
SS VF-F/M CARB INC |
|
32 |
3522.48 |
3523.47 |
0.98 |
165.0 |
0.0 |
11.9 |
0.219 |
0 |
0 |
0.058 |
0.408 |
SS VF-F/M CARB INC |
|
33 |
3523.47 |
3524.48 |
1.02 |
586.0 |
0.0 |
66.0 |
0.219 |
0 |
0 |
0.082 |
0.411 |
|
|
34 |
3524.48 |
3525.47 |
0.98 |
1035.0 |
0.0 |
395.0 |
0.244 |
0 |
0 |
0.051 |
0.391 |
SS VF-F |
|
35 |
3525.47 |
3526.48 |
1.02 |
514.0 |
0.0 |
187.0 |
0.199 |
0 |
0 |
0.073 |
0.360 |
|
|
36 |
3526.48 |
3527.47 |
0.98 |
526.0 |
0.0 |
89.0 |
0.205 |
0 |
0 |
0.046 |
0.481 |
SS VF-M |
|
37 |
3527.47 |
3528.16 |
0.69 |
1375.0 |
0.0 |
208.0 |
0.216 |
0 |
0 |
0.042 |
0.548 |
SS VF-M PY CARB |
|
38 |
3528.16 |
3528.88 |
0.72 |
287.0 |
0.0 |
95.0 |
0.207 |
0 |
0 |
0.066 |
0.462 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arithmetic Averages |
0.78 |
618.8 |
0.0 |
240.7 |
0.253 |
0.0 |
0.0 |
0.095 |
0.443 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|












 By dividing each weight by its respective density and
adjusting each result for the total weight of the sample, the
volume fraction of each is obtained. Porosity is the sum of
water plus oil volume fractions Because the bound water in
the clay is driven off by the drying sequences, this porosity is
the total porosity.
By dividing each weight by its respective density and
adjusting each result for the total weight of the sample, the
volume fraction of each is obtained. Porosity is the sum of
water plus oil volume fractions Because the bound water in
the clay is driven off by the drying sequences, this porosity is
the total porosity. Assuming clay bound water is driven off by heating and drying,
then PHIcore equals total porosity. From comparison to log
analysis results, it appears that some clay bound water remains
in many cases, so PHIcore lies between total and effective
porosity from log analysis.
Assuming clay bound water is driven off by heating and drying,
then PHIcore equals total porosity. From comparison to log
analysis results, it appears that some clay bound water remains
in many cases, so PHIcore lies between total and effective
porosity from log analysis.