|
 WATER ANALYSIS METHODS
WATER ANALYSIS METHODS
Laboratory water
analysis is an essential measurement required for accurate water
saturation calculations from log data. Water samples are collected
from drill stem tests or produced fluids. In the case of produced
fluids, the water should be captured from the flow line and
separated later from the oil. Samples from separators or treaters
may not be representative of formation water due to contamination.
Samples from drill stem tests are usually taken at the top, middle,
and bottom of the test recovery. The bottom sample should have the
least contamination from drilling fluid invasion. The top sample
will have the most contamination.
Laboratories
usually measure from 9 to 15 of the individual ions in a water
sample, recorded in milligrams/litre (mg/l) or grams/cubic meter
(g/m3). These two sets of units are equivalent: 1 mg/l =
1 g/m3.
At low to moderate concentrations, one mg/l is very
close to 1 part per million (ppm) so mg/l and ppm tend to be used
interchangeably. The difference is that ppm = mg/l divided by the density of
the water.
In older reports, results were quoted in
grains per gallon (gpg) One grain per US gallon equals 17.1 mg/l or
approximately 17.1 ppm.
The cations (positive ions) are measured by ion
chromatograph. These are Sodium (Na), Potassium (K), Calcium (Ca),
Magnesium (Mg), Iron (Fe), and sometimes Barium (Ba), Strontium (Sr),
or Boron (Bo). The anions (negative ions) cannot be measured by ion
chromatograph so Chloride (Cl) and sometimes Iodide (I) and Bromide
(B) are still measured by titration. Bicarbonate (HCO3)
and Carbonate (CO3) are calculated from the volume of
acid required to reduce the pH to 8.3 (for CO3) and 4.5
(for HCO3). Sulphate (SO4) is calculated by
adding a volume of Barium Chloride and then measuring the turbidity
of the solution. The sum of all of these measured ions becomes the
calculated total dissolved solids (TDS).
They also measure, in a routine analysis, the pH,
relative density, and resistivity (Rw) of the water sample. The Rw
is measured in ohm-m and they will record the temperature at which
it was measured. This temperature will be used to adjust the
measured Rw to a common "laboratory temperature", usually 25 Celsius
or 77 Farenheit. Some labs use different standard temperatures.
Some labs also provide mmol/l (or moles/m3).
mg/l (or g/m3) divided by the molar mass of the ion
equals mmol/l (or moles/m3). Since mg/l is the same thing
as g/m3, mmol/l is the same thing as mol/m3.
Molar mass is derived from the atomic weight of the ion on the
Periodic Table. For instance, the atomic weight of S is 32 and the
atomic weight of O is 16, so the molar mass of SO4= 32 +
4 * 16 = 96.
Most labs calculate milli-equivalents (MEQ). MEQ
equals mmol/l or moles/m3 multiplied by the valence or
charge of the ion. SO4 has a negative charge of 2 so 1
mmol/l of SO4 equals 2 MEQ of SO4. Sodium
(Na) has a positive charge of 1, so 1 mmol/l of Na equals 1 MEQ of
Na.
The logging company charts that convert ppm to Rw are
based on ppm of pure NaCl. This is because the most common formation
waters found in the world are NaCl based. These charts will give you
the wrong Rw if the fluid is a mud filtrate which is mostly Na2SO4
or if the fluid is Sodium Bicarbonate type formation water.
The diagram at the bottom of the water analysis is
called a Stiff Diagram. It is a graphical representation of the
different ions. The shape of the Stiff Diagram can become a
“fingerprint” which can allow us to distinguish whether the fluid is
formation water or an introduced fluid, and can often distinguish
the zone from which the formation water was produced.
 SAMPLE WATER ANALYSIS REPORT
SAMPLE WATER ANALYSIS REPORT
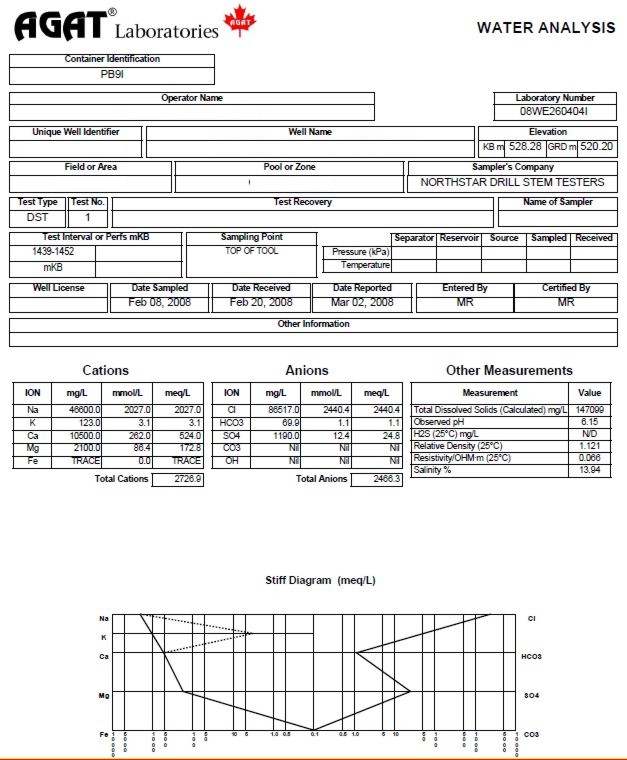
Water analysis report from a drill
stem test recovery, showing chemical analysis, calculated and
measured water resistivity, and Stiff diagram of chemical analysis.
This is a fairly salty formation water with salinity of 146,000
parts per million (ppm) and a resistivity of 0.066 @ 25C.
 WATER SAMPLE CONTAMINATION
WATER SAMPLE CONTAMINATION
Contamination of water samples by drilling fluid
invasion is common and the Stiff Diagram helps to spot this
problem. For instance, a typical gel-chem type mud filtrate recovery
will have Na in MEQ divided by Cl in MEQ of 5 or greater. Most
contamination problems require some experience and a supply of Stiff
Diagram fingerprints that are reasonably consistent.
For more
information on fingerprinting water recoveries, please contact Opus
Petroleum Engineering Ltd.,
www.opuspetroleum.com.
The Canadian
Water Resistivity Catalog is well screened, but field samples may be
contaminated. The following rules of thumb are useful in detecting
mud filtrate contamination or meteoric water recharge.
1. Mg/l and
ppm are approximately the same thing except in very saline waters.
2. Most gel-chem
mud filtrates are usually from 3000 to 8000 mg/l TDS.
3. When the
log header says gel-chem mud, they might mean gyp’ed-up mud. Gyp’ed-up
mud usually has soda ash added to compensate for drilling through
anhydrites. Gyp’ed-up mud filtrates are usually from 10,000 to
25,000 mg/l TDS.
4. KCl mud
filtrates are usually from 30,000 to 50,000 mg/l TDS with lots of K
and lots of Cl.
5. Potassium
Sulphate mud filtrates are usually from 50,000 to 80,000 mg/l TDS
with lots of K and lots of SO4.
6.
Salt-saturated mud filtrates are usually 300,000 mg/l or higher.
7. Generally
speaking, formation waters increase in salinity with depth but see
#12.
8. Each zone
should have a unique formation water “fingerprint” or Stiff Diagram
unless it is hydraulically connected to another zone.
9. This
formation water “fingerprint” may change with location in the
basin.
10. Most
formation waters have a milli-equivalent Na/Cl
ratio of 0.6 to 1.2.
11. Many
formation waters are fresher than expected as they are affected by
fresh water recharge from the surface. These recharge waters have a
distinctive fingerprint which is high in bicarbonates and the milli-equivalent
Na/Cl ratio is usually between 2 and 3. These fresh waters have been
found in formations as deep as the Devonian and can under-run more
saline formation waters.
12. Never
rely on one water analysis as being representative of the formation
water in a particular pool and field. Try to find at least three
water samples in your pool that have formation water
characteristics, are close to the same TDS and have similar
“fingerprints”. Then compare the Rw on your samples to the ones in
the catalog.
Agat Lab in Calgary uses a "Smart
Chart", incorporating these rules, to help identify clean
water samples from those contaminated by mud filtrate or other
chemicals.
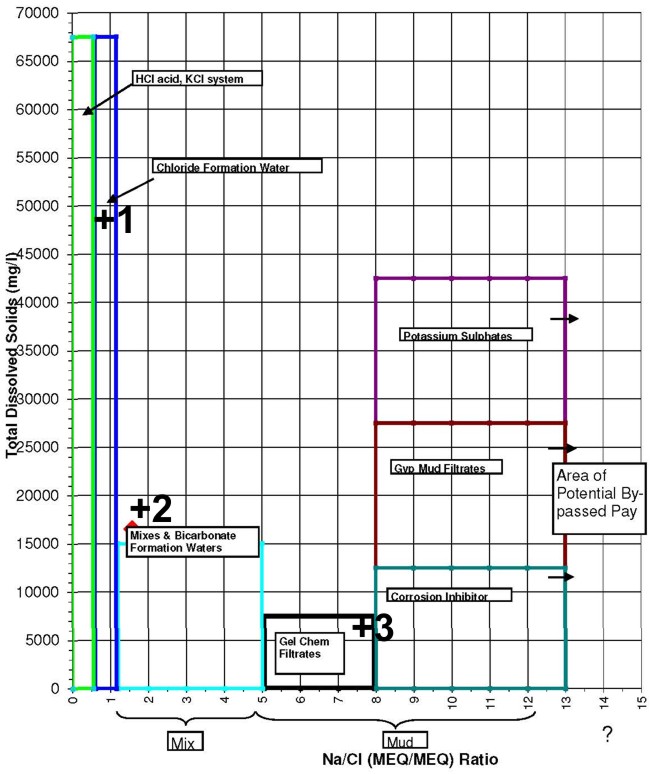
This crossplot of TDS versus the Na/Cl ratio helps check for
contamination. Data point 1 is in the formation water category.
Point 2 is either naturally high in bicarbonates or contaminated by
some gyp-based mud invasion. Point 3 is mostly gel-based mud
filtrate.
 Equivalent NaCl
Water Salinity
from Water Analysis
Equivalent NaCl
Water Salinity
from Water Analysis
The
resistivity of a water sample can be calculated from its
chemical analysis. To do this, an equivalent NaCl concentration
must be determined based on the ionic activity of each ion.
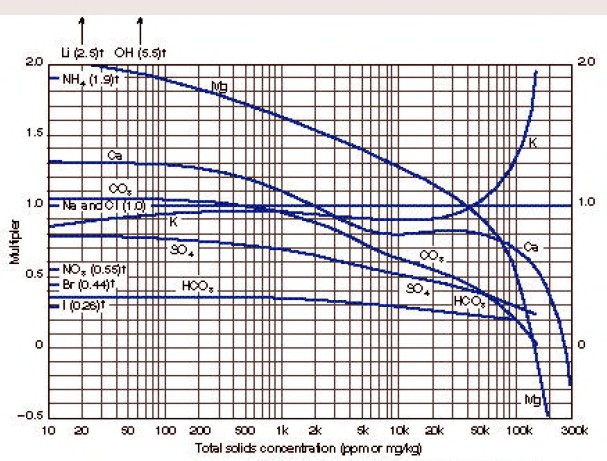
Enter chart with total solids concentration of the sample in ppm
(mg/kg) to find weighting factors for each ion present. The
concentration of each ion is multiplied by its weighting factor, and
the products for all ions are summed to obtain equivalent NaCl
concentration.
The math is
pretty simple:
1: TDS = SUM (IONi)
2:
WSe = SUM (IONi * FACTRi)
Where:
TDS = total dissolved solids (ppm)
IONi = ion concentration of ith component (ppm)
FACTRi = multiplier factor for ith component (ppm)
WSe = equivalent NaCl concentration (ppm)
 NUMERICAL EXAMPLE:
NUMERICAL EXAMPLE:
Assume formation-water sample analysis
460 ppm Ca,
1400 ppm SO4
19,000 ppm Na plus Cl.
Total dissolved solids concentration
TDS = 460 + 1400 + 19,000 = 20,860 ppm
Entering the chart with this total solids concentration
Ca multiplier = 0.81
SO4 multiplier = 0.45
Na+CL multiplier = 1.00
Equivalent NaCl concentration = 460 ´ 0.81 + 1400 ´ 0.45 + 19,000 ´
1.0 = 20,000 ppm.
 Water Salinity from
Chloride Content Water Salinity from
Chloride Content
Sometimes salinity is reported at the well site in ppm Chlorides
instead of ppm NaCl equivalent.
6: WSa = Ccl * 1.645
Where:
Ccl = water salinity (ppm Cl)
WSa = water salinity (ppm NaCl)
 COMMENTS:
COMMENTS:
Use this relationship when chloride content of the water sample
is known. Usually Cl content is derived at the
well site from a drill stem test recovery. It is useful as a
first approximation until the water sample is analyzed more
accurately at a laboratory. The relationship is for pure NaCl
solutions and the factor may be higher or lower if other ions
are present.
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
1. Chloride concentration to salinity.
WS = 11,600 ppm Cl * 1.645 = 19,000 ppm NaCl
 Water Resistivity from Salinity
AT ANY TEMPERATURE
Water Resistivity from Salinity
AT ANY TEMPERATURE
Crain's Model is used to convert a lab measured salinity
to a formation water resistivity (RW) at any specific temperature (FT) in degrees Fahrenheit.
The result is abbreviated as RW@FT
throughout this Handbook. You can use equation 5 to convert a
salinity to any arbitrary temperature, for example 75F or 77F
(roughly 25C) to find the resistivity at laboratory conditions.
1: FT = SUFT + (BHT - SUFT) / BHTDEP * DEPTH
2: IF LOGUNITS$ = "METRIC"
3: THEN FT1 = 9 / 5 * FT + 32
4: OTHERWISE FT1 = FT
5: RW@FT = (400000 / FT1 / WS) ^ 0.88
 SALINITY FROM WATER RESISTIVITY
SALINITY FROM WATER RESISTIVITY
Invert Crain's equation to solve for WS given RW at a a specific
temperature FT1.
6:
WS = 400000 / FT1 / ((RW@ET) ^ 1.14)
Where:
BHT = bottom hole temperature (degrees Fahrenheit or Celsius)
BHTDEP = depth at which BHT was measured (feet or meters)
DEPTH = mid-point depth of reservoir (feet or meters)
FT = formation temperature (degrees Fahrenheit or
Celsius)
FT1 = formation temperature (degrees Fahrenheit)
RW@FT = water resistivity at formation temperatures (ohm-m)
SUFT = surface temperature (degrees Fahrenheit or Celsius)
WS = water salinity (ppm NcCl)
 COMMENTS:
COMMENTS:
Use this relation if salinity is known from laboratory measurements
to obtain RW from lab data at any temperature.
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
1. Salinity to water resistivity.
RW@FT = (400000 / 102'F / 20,000 ppm) ^ 0.88 = 0.238 ohm-m @
102'F
(rounded to three significant digits)
2.
Water resistivity to salinity.
WS = 400,000 / 102'F / ((0.250 ohm-m) ^ 1.14) = 19,000 ppm NaCl
(rounded to three significant digits)
 Water Resistivity from Salinity
at Lab Temperature Water Resistivity from Salinity
at Lab Temperature
These models generate RW at laboratory temperature of 75F or 25C.
Crain's Method (1974)
1: RW@75F = (400000 / 75 / WS) ^ 0.88
Bateman and Konen Method (1977)
2: RW@75F = 0.0123 + (3647.5 / WS^0.955)
Kennedy's Method (2015)
3: RW@75F = 1 / (24.30853 - 0.0364 *
(0.1 * WS - 29.46515957) - 0.02922 * (0.1 * WS - 29.46515957)^2)
 SALINITY FROM WATER RESISTIVITY
SALINITY FROM WATER RESISTIVITY
Crain's Method (1974)
4:
WS = 400000 / 75 / ((RW@75) ^ 1.14)
Baker Atlas Method (2002)
5: WS = 10 ^ ((3.562 - (Log (RW@75
- 0.0123))) / 0.955)
 COMMENTS:
COMMENTS:
For all
practical purposes, the three models give the same RW value (see
Graph 1 below). There are minor differences above 150,000 ppm NaCl
which can only be seen when water resistivity is converted to water
conductivity (see Graph 2 below).
The effect on water saturation (SW%) is not very significant (+/-
0.5% SW at low SW, +/- 2% SW at high SW, at 200,000 ppm NaCl).
The 10 significant digits used in the Kennedy equation give a false
sense of accuracy that is not warranted.
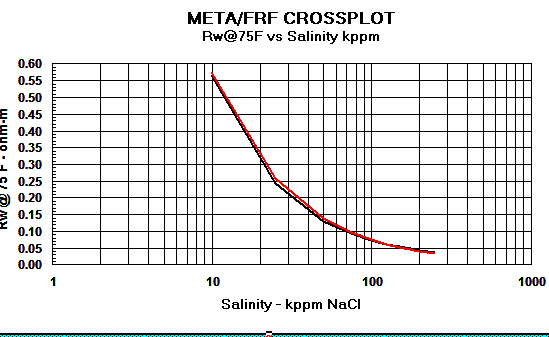
Graph 1:
Rw Models - Red line = Crain, Black line
= Bateman and Konen, Blue line = Kennedy
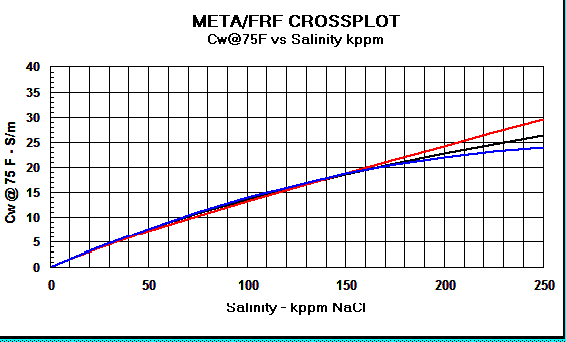
Graph 2:
Cw Models - Red
line = Crain, Black line = Bateman and Konen, Blue line =
Kennedy.
The differences above 150,000 ppm NaCl have little impact on water
saturation.
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
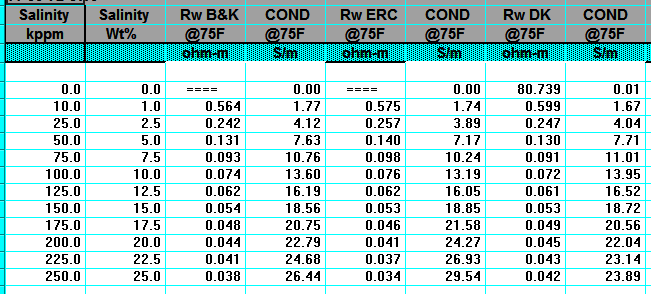
 RW from Water Catalogs
RW from Water Catalogs
Water catalogues published by your local well logging society
or similar catalogues created by searching in-house data bases
are a necessary tool for well log analysis.
A sample is shown below.
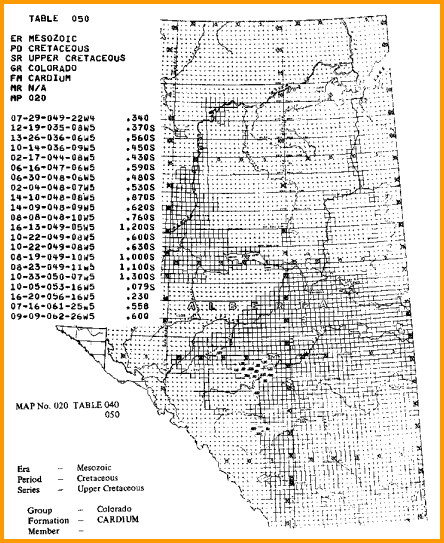
A sample of RW data from a water resistivity catalog, data is tabulated and also
posted on
a map, and is based on a standard temperature of 25 degrees Celsius
(77 degrees Fahrenheit).
 Water
resistivity values in a catalog are recorded at a standard
temperature, usually 75F or 77F (25C). Since water resistivity varies
inversely with temperature, the catalog values must be
transformed to a new value representing water resistivity at
formation temperature (RW@FT) -- see
next Section. Water
resistivity values in a catalog are recorded at a standard
temperature, usually 75F or 77F (25C). Since water resistivity varies
inversely with temperature, the catalog values must be
transformed to a new value representing water resistivity at
formation temperature (RW@FT) -- see
next Section.
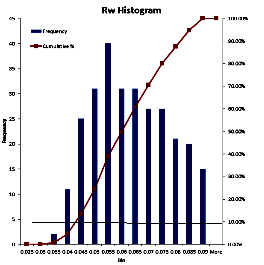
To use data from a water catalogue, it is usually necessary to
do a little filtering. Nearly everything that can go wrong will
raise the RW value recorded in the catalogue. Usually the
minimum value from nearby offset wells is the best choice. It
may be useful to gather all the values for the reservoir for a
radius of 3 to 6 miles (5 to 10 Km) and prepare a histogram. On
the histogram, find the point that represents the lower decile
(10% of the data values are less than this value). Take the
average of the data in this decile. You may want to eliminate
obvious "impossible" values before you make the histogram.
The
following relationships are needed to manipulate water resistivity
data prior to calculations of water saturation.
1. Arps Method (1953)
1:
FT = SUFT + (BHT - SUFT) / BHTDEP * DEPTH
2: KT1 = 6.8 for English units
KT1 = 21.5 for Metric units
3: RW@FT = RW@TRW * (TRW + KT1) / (FT +
KT1)
4: RMF@FT = RMF@TRW * (TRW +
KT1) / (FT + KT1)
5: RMC@FT = RMC@STRW + (TRW * KT1) / (FT + KT1)
Where:
SUFT = surface temperature for temperature gradient
(degrees Fahrenheit or Celsius)
BHT = bottom hole temperature (degrees Fahrenheit or Celsius)
BHTDEP = depth at which BHT was measured (feet or meters)
DEPTH = mid-point depth of reservoir (feet or meters)
FT = formation temperature (degrees Fahrenheit or Celsius)
RMC@FT = mud cake resistivity at formation temperature (ohm-m)
RMC@TRW = mud cake resistivity at surface temperature (ohm-m)
RMF@FT = mud filtrate resistivity at formation temperature (ohm-m)
RMF@TRW = mud filtrate resistivity at surface temperature (ohm-m)
RW@FT = water resistivity at formation temperatures (ohm-m)
RW@TRW = water resistivity at surface temperature (ohm-m)
TRW = temperature at which water was measured (degrees Fahrenheit or Celsius)
2. Hilchie Model (1984) ALL temperatures in Fahrenheit.
6: KT1 = 10^ ( --0.340396 * log(RW@TRW)
+ 0.641427)
7:
FT1 = SUFT + (BHT - SUFT) / BHTDEP * DEPTH
8: RW@FT = RW@TRW * (TRW + KT1) / (FT1 +
KT1)
9: RMF@FT = RMF@TRW * (TRW +
KT1) / (FT1 + KT1)
10: RMC@FT = RMC@STRW + (TRW * KT1) / (FT1 + KT1)
Where:
FT1 = formation temperature (degrees Fahrenheit ONLY)
COMMENTS:
Use
these relations when RW@TRW
is known from measured data. This transformation can be made on
the chart below. The Hilchie model accounts for the slight
curvature at low and high temperatures on the chart, but Arps model
is quite sufficient for practical petrophysics.
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
1. Water resistivity at formation temperature.
English units example:
RW@FT = (0.32 ohm-m @ 77'F) * (77 + 6.8) / (102 + 6.8) = 0.25
ohm @ 102'F
Metric
units example:
RW@FT = (0.32 ohm-m @ 25'C) * (25 + 21.5) / (39 + 21.5) = 0.25
ohm-m @ 39'C
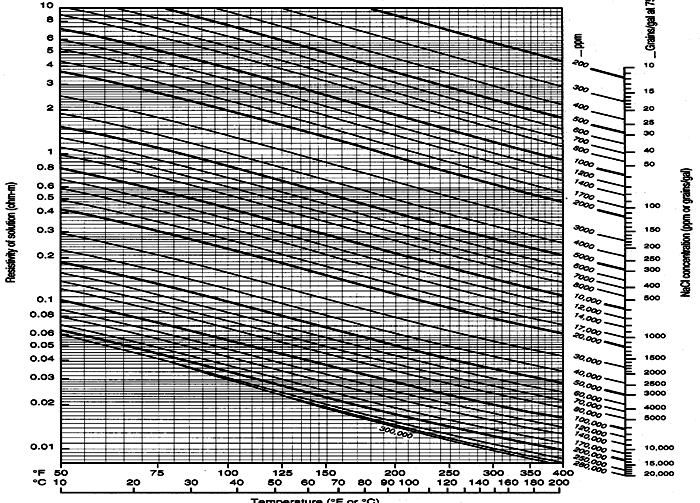
Schlumberger Chart GEN-9: Water resistivity - Temperature - Salinity relationships
 ESTIMATING
SURFACE AND FORMATION TEMPERATURES ESTIMATING
SURFACE AND FORMATION TEMPERATURES
Temperature
measurements specific to your area of interest are going to
sparse and you will have to do some searching for useful data.
The map below gives a good idea of what to use for surface
temperature (SUFT). Temperature versus depth data from log
headings can be plotted to estimate a best fit temperature
gradient line. It doesn't have to be a straight line. See
representative graphs below. In areas with sparse data, use the
temperature gradient maps supplied below.
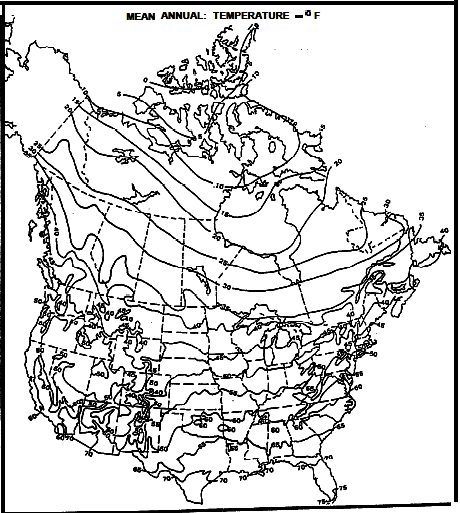
Mean Annual Surface Temperature Map for North America - degrees F
The 40 deg F contour follows roughly along the US-Canada border
except along the coast lines.
Contour interval is 5 deg F.
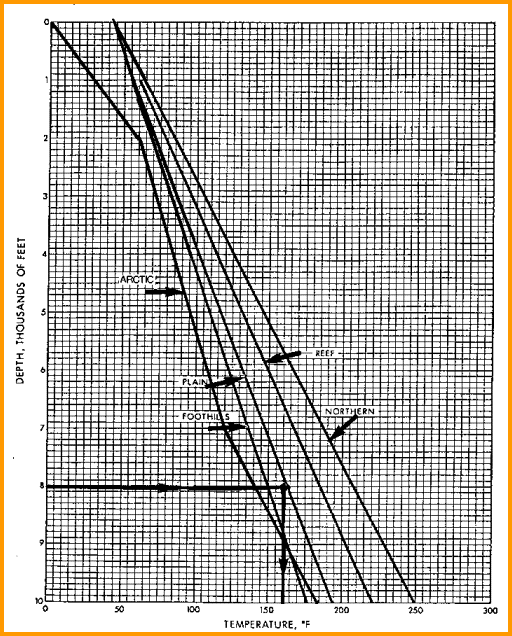
Typical Depth - Temperature profiles. Create your own by
best fit of BHT vs BHTDEP from data on log
headings or DST reports.
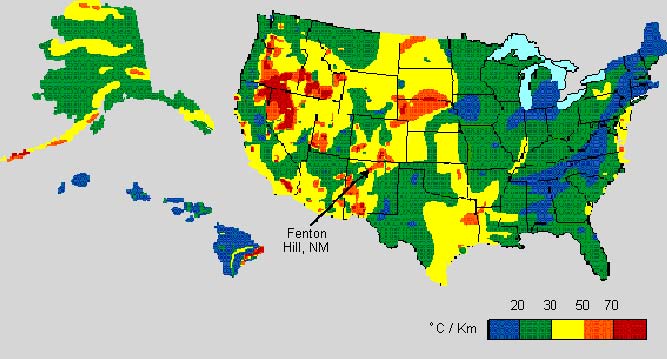
Temperature gradient for USA -
degrees Celsius per 1000 meters,
North American Heat Floe Map
(3 MB)
Legible Legend for NA Map
Temperature at 5000 meters for
Australia
 META/LOG "RW" SPREADSHEET -- Water Resistivity Calculations
META/LOG "RW" SPREADSHEET -- Water Resistivity Calculations
This spreadsheet calculates RW at formation temperature using 5
different methods.
Download this spreadsheet:
SPR-07 META/LOG WATER RESISTIVITY (RW) CALCULATOR
Calculate water resistivity (RW),
5 methods,
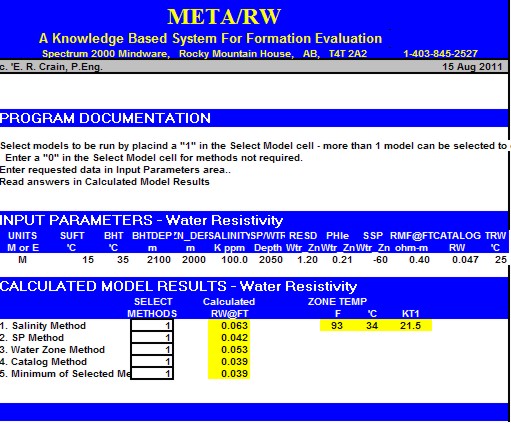
Sample of "META/RW" for calculating water resistivity from various
methods.
|









 Water
resistivity values in a catalog are recorded at a standard
temperature, usually 75F or 77F (25C). Since water resistivity varies
inversely with temperature, the catalog values must be
transformed to a new value representing water resistivity at
formation temperature (RW@FT) -- see
next Section.
Water
resistivity values in a catalog are recorded at a standard
temperature, usually 75F or 77F (25C). Since water resistivity varies
inversely with temperature, the catalog values must be
transformed to a new value representing water resistivity at
formation temperature (RW@FT) -- see
next Section.




