PETROPHYSICAL MODELS - HOW THE MATH WORKS
The rock-fluid model used for the analysis methods described in this Handbook is shown in the illustration below. From this model, we can generate a series of equations that can be used to calculate the petrophysical properties of a rock. These equations have been derived by many researchers across a long period of years. Some equations are tuned to local areas, and may not be universally applicable. The mathematical algorithms selected for inclusion in this Handbook were chosen for their universal applicability, although many regionalized variations probably exist for most of them. Because you might need to modify existing models, or develop a new one of your own, the basic reservoir model should always be in the back of your mind.

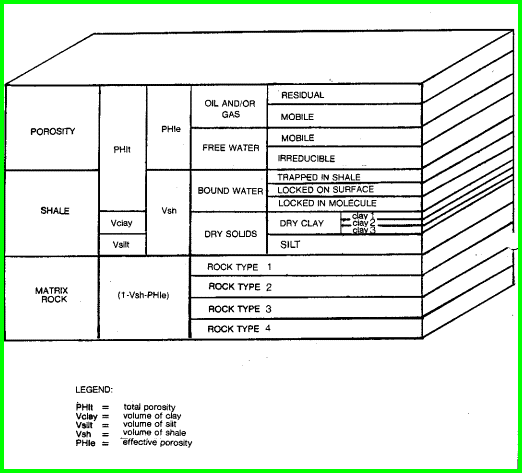
The physical model shown below is critical in the understanding of how logs respond to the different components of the rock. To see the effect of variations in lithology, porosity, and fluid type, see Log Response Chart (PDF). You will need to view this file at 100% zoom in Acrobat to read the curves. Remember that the density and neutron are shown on a Limestone equivalent scale, so sandstones show crossover even when there is no gas.


 

The Rock-Fluid Model for Petrophysical Analysis

LOG RESPONSE EQUATION
The response of an individual log to the rock-fluid model is defined by the log response equation. The usual log response equations are of the form:

This response equation will work for sonic travel time, density, or density porosity, neutron porosity, gamma ray (and the spectrolog curves - uranium, thorium and potassium), resistivity (if Sxo is replaced by Sw for deep resistivity logs), the electromagnetic propagation log, the thermal decay time log, and the photoelectric effect (if PE * DENS is used). It will also work for various derived logs described in later chapters of this handbook.

The response equations can be used in several ways. One is to find out what a log would read under a hypothetical set of circumstances. Another way is to calculate one unknown in the equation, for example porosity or shale volume, by using a log reading and assuming the other terms to be known or derivable from some other response equations. A third approach is to use sets of response equations simultaneously to determine as many unknowns as possible from the available log data.

Some terms in the response equation for certain logs go to zero. This is what makes it possible, for example, to calculate the shale volume from the gamma ray response. Both the water and hydrocarbon terms go to zero, since neither of these components has any gamma ray contribution. By re-arranging terms and further assuming that porosity is small, we get:

    1. VSHgr = (GR - GRmatrix) / (GRshale - GRmatrix)

Here GR, GRshale, and GRmatrix are read from appropriate places on the gamma ray log to calculate shale volume.

In other cases, we sometimes lump two terms together, as for water and oil in the sonic log equation for porosity. This strategy eliminates the need to know water saturation prior to knowing porosity. This approach will fail if gas is present because the water and gas contributions are too dissimilar.

The algorithms in following chapters attempt to resolve as many of the unknowns as possible using these piecewise techniques. Where this is inappropriate, sets of two or three simultaneous equations are solved, with the final solution being given. It will not always be obvious that simultaneous response equations were used, but ALL deterministic log analysis methods rely on this approach. What we have done here is eliminate the repetitive derivation of the solution, and present instead the finished product, ready for inclusion in a calculator, spreadsheet or computer program.

The borehole environment, invasion, and rock model define the log analysis problem. Logging tools define most of the data available to analyze the model. With many analysis methods to choose from, there are usually many possible answers. It is the analyst's job to select the method and model that best describe the problem to be solved. Adjustments to the basic model presented here are therefore plausible, and may be essential.